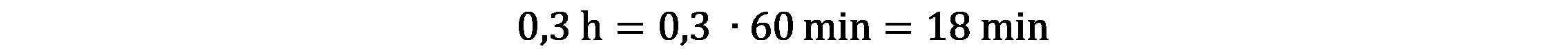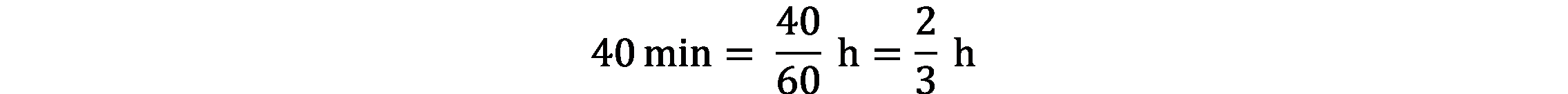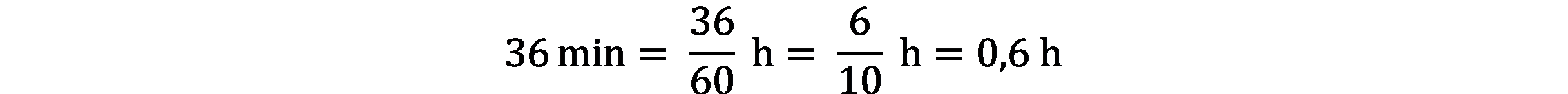Kochani Uczniowie klas szóstych,
zaczynamy nowy tryb pracy. Dla niektórych będzie to nowa lekcja, dla innych utrwalenie. Wkrótce jednak wszystko się wyrówna. Nie poddawajcie się i podejmijcie wyzwanie. Lekcje przepisujcie do zeszytu zgodnie z numeracją podaną niżej. Jeżeli będziecie mieć problemy z rozwiązaniem zadań jesteśmy do Waszej dyspozycji. Pytania możecie zadawać drogą e-mail, przez dziennik elektroniczny lub przez aplikację Teams.
Mirosława Modzelewska miroslawa.modzelewska@sp2gk.onmicrosoft.com
Anna Nowak anna.nowak@sp2gk.onmicrosoft.com
Jolanta Skolimowska jolanta.skolimowska@sp2gk.onmicrosoft.com
Anna Wilk anna.wilk@sp2gk.onmicrosoft.com
WAŻNE! Do sprawdzenia będziecie przesyłać tylko wskazane przez nauczyciela zadania.
Na odesłanie zadań macie 2 dni robocze od dnia, w którym odbywa się dana lekcja. Oznacza to, że jeżeli lekcja wypada w poniedziałek to pracę należy odesłać do środy, jeśli we wtorek to do czwartku, jeśli we środę to do piątku, jeśli w czwartek to do poniedziałku, jeśli w piątek to do wtorku).
Jeżeli nie możecie odesłać pracy w tym terminie, to koniecznie skontaktujcie się ze swoją nauczycielką.
Jeśli nie macie podręcznika w domu, to możecie skorzystać z udostępnionego przez wydawnictwo na stronie: https://ebooki.nowa
Tydzień obowiązywania: 22 – 25 czerwca 2020 r.
Lekcja 44
Temat: Odżywianie.
Cel lekcji: Nauczę się korzystać z informacji zawartych na produktach spożywczych i obliczać kaloryczność posiłków.
Potraficie już korzystać z różnego rodzaju tabeli, diagramów, cenników. Zapewne zauważyliście, że na opakowaniu każdego produktu spożywczego jest tabelka, w której podane są informacje dotyczące zawartości białka, cukrów, tłuszczu i kaloryczności w 100 g tego produktu. Mając te informacje możemy zaplanować swój posiłek tak, aby był zdrowy i zawierał właściwe proporcje niezbędnych składników.
Pamiętajcie też, że zapotrzebowanie energetyczne człowieka zależy od jego wieku i trybu życia jaki prowadzi. Wyższe jest w przypadku osób, które wykazują się dużą aktywnością fizyczną.
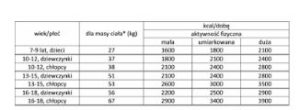
Wykonaj ćw. 2 i 3 na str. 160 w ćwiczeniach.
*Wersja do wydruku: Lekcja 44 – Odżywianie
Lekcja 45
Temat: Utrwalenie wiadomości o bryłach.
Ceł lekcji: Utrwalę wiadomości o graniastosłupach rozwiązując zadania online.
Dział matematyki poświęcony bryłom sprawia uczniom sporo problemów. Dlatego dzisiaj powtórzymy i utrwalimy zdobyte wiadomości rozwiązując zadania online.
Przypomnij sobie, jak obliczamy powierzchnię prostopadłościanu:
https://www.matzoo.pl/klasa6/pole-powierzchni-prostopadloscianu-rozgrzewka_34_636
A teraz powtórz obliczanie powierzchni innych graniastosłupów:
https://www.matzoo.pl/klasa6/pole-powierzchni-graniastoslupa-prostego_34_514
Na koniec przypomnij sobie, jak obliczamy objętość prostopadłościanu:
https://www.matzoo.pl/klasa6/objetosc-prostopadloscianu_34_516
*Wersja do wydruku: Lekcja 45 – Powtórzenie wiadomości o bryłach
Lekcja 46
Temat: Gry i zabawy matematyczne.
Cel lekcji: Utrwalę umiejętności matematyczne rozwiązując łamigłówki.
Za kilka dni rozpoczynają się wakacje. Czekaliśmy na nie z utęsknieniem, zwłaszcza, że ostatnie miesiące były dla nas wszystkich niełatwe. Ostatnia lekcja matematyki w tym roku szkolnym będzie nietypowa, bo będzie zabawą, ale zabawą wymagającą pewnych umiejętności matematycznych. Na pewno każdy z Was spotkał się z „zapałczanymi” zagadkami. Przypomnij sobie znaki rzymskie i rozwiąż zadania – zagadki:
https://www.matzoo.pl/lamiglowki/zapalki-poziom-1-rozgrzewka_40_420
Na poprawę humoru przeczytaj kilka matematycznych anegdot:
http://www.math.edu.pl/anegdoty
To już nasza ostatnia lekcja matematyki w tym roku szkolnym.
Bardzo różnił się przebieg tych 46 lekcji od poprzedniego, wszyscy musieliśmy się nauczyć pracować w inny sposób.
Wymagało to do Was większej samodzielności, obowiązkowości, a także wsparcia Waszych Rodziców.
Mamy nadzieję, że staraliście się jak najwięcej skorzystać z Lekcji zdalnych umieszczanych na stronie internetowej szkoły. Będziecie mogli jeszcze do nich powracać (może warto mieć je wydrukowane?)
Nam też bardzo brakowało bezpośredniego kontaktu z Wami.
Dziękujemy Wam za Waszą współpracę.
Życzymy Wam udanych, radosnych wakacji i liczymy na spotkanie z Wami we wrześniu.
Do zobaczenia! 😊
Nauczycielki matematyki.
*Wersja do wydruku: Lekcja 46 – Gry i zabawy matematyczne.
Lekcja 40 Lekcja 41Lekcja 42 Lekcja 43
Tydzień obowiązywania: 15 – 19 czerwca 2020 r.
Lekcja 40
Temat: Plan, mapa i skala – rozwiązywanie zadań tekstowych.
Cel lekcji: Utrwalę zdobyte umiejętności w sytuacjach praktycznych.
Na ostatniej lekcji przypomnieliśmy sobie pojęcie skali, a także zamienialiśmy skalę liczbową na skalę mianowaną. Dzisiaj skupimy się na obliczaniu rzeczywistej odległości między dwoma punktami na podstawie mapy i jej skali. Żeby obliczyć tę odległość trzeba najpierw zmierzyć ją na mapie, a także wyrazić skalę mapy w postaci skali mianowanej.
Jeśli nie pamiętasz, jak to robimy, zajrzyj do notatki z ostatniej lekcji.
Uwaga: Ponieważ od 15 czerwca oddajecie do biblioteki wypożyczone podręczniki, prace do samodzielnego wykonania będą zadawane tylko w ćwiczeniach.
Wykonaj: ćw. 4, 5 i 6 na str. 146 oraz ćw. 8 na str. 147 w zeszycie ćwiczeń.
Dla chętnych: ćw. 10 na str. 148 w zeszycie ćwiczeń
*Wersja do wydruku: Lekcja 40 – Plan, mapa i skala – rozwiązywanie zadań tekstowych.
Lekcja 41
Temat: Zakupy.
Cel lekcji: Przypomnę sobie i utrwalę obliczenia pieniężne.
Umiejętności matematyczne bardzo często wykorzystujemy w życiu codziennym. Jedną z takich sytuacji jest obliczanie wartości zakupów, albo ceny jednostkowej towaru. Wykonywaliśmy już takie obliczenia, a teraz je sobie przypomnimy.
Zapisz w zeszycie:
Zad. 1
Oblicz ile kosztuje 2,5 kg jabłek w cenie 4,50 zł za 1 kg.
I sposób:
1 kg – 4,50 zł
2,5 kg – 2,5 · 4,50 zł = 11,25 zł
II sposób:
1 kg – 4,50 zł
0,5 kg – 4,50 zł : 2 = 2,25 zł
2,5 kg – 2 · 4,50 zł + 2,25 zł = 9 zł + 2,25 zł = 11,25 zł
Odp. Za 2,5 kg jabłek trzeba zapłacić 11,25 zł.
Zad. 2
Za 30 dag sera żółtego zapłacono 9,60 zł. Ile kosztuje 1 kg tego sera?
I sposób:
30 dag = 0,3 kg – 9,60 zł
9,60 zł : 0,3 = 96 zł : 3 = 32 zł
II sposób:
30 dag – 9,60 zł
10 dag – 9,60 zł : 3 = 3,20 zł
1 kg = 100 dag = 10 · 10 dag – 10 · 3,20 zł = 32 zł
Odp. 1 kilogram tego sera kosztuje 32 zł.
Wykonaj: ćw. 2 na str. 151 i ćw. 3 na str. 152 w zeszycie ćwiczeń.
Dla chętnych: ćw. 6 na str. 153 w zeszycie ćwiczeń.
*Wersja do wydruku: Lekcja 41 – Zakupy
Lekcja 42
Temat: Działki, domy, mieszkania.
Cel lekcji: Wykorzystam zdobyte umiejętności w sytuacjach praktycznych.
Potraficie obliczyć powierzchnię prostokąta i innych wielokątów, znacie jednostki pola. Dzisiaj wykorzystamy te umiejętności w rozwiązywaniu zadań. Powierzchnię mieszkania, domu, niewielkiej działki wyrażamy w m². Do określenia dużych powierzchni używamy większych jednostek. Te jednostki to ar (a), hektar (ha) i km². Ar to powierzchnia kwadratu o boku 10 m, hektar to powierzchnia kwadratu o boku 100 m. Największą jednostką jest km² czyli powierzchnia kwadratu o boku 1 km.
Zapisz w zeszycie:
1 a = 100 m²
1 ha = 10 000 m² 1 ha = 100 a
1 km² = 1 000 000 m² 1 km² = 100 ha = 10 000 a
Wykonaj: ćw. 2 i 3 na str. 154 oraz ćw. 4 na str. 155 w zeszycie ćwiczeń.
Dla chętnych: ćw. 5 na str. 155 w zeszycie ćwiczeń.
*Wersja do wydruku: Lekcja 42 – Działki, domy, mieszkania
Lekcja 43
Temat: Podróż.
Cel lekcji: Wykorzystam zdobyte umiejętności w rozwiązywaniu zadań związanych z podróżą.
Potraficie wykonywać obliczenia zegarowe, korzystać z różnych tabeli, cenników, rozkładów jazdy. Umiecie posługiwać się mapą i korzystać ze skali. Te umiejętności wykorzystacie dzisiaj w rozwiązywaniu zadań.
Wykonaj: ćw. 2 i 4 na str. 156 oraz ćw. 5 na str. 157 w zeszycie ćwiczeń.
Dla chętnych: ćw. 8 na str. 158 w zeszycie ćwiczeń
*Wersja do wydruku: Lekcja 43 – Podróż
Tydzień obowiązywania: 08 – 12 czerwca 2020 r.
Lekcja 38
Temat: Korzystanie ze wzorów – ćwiczenia.
Cel lekcji: Nauczę się zapisywać wzór na podstawie opisu słownego.
Wiecie już, że wzór, to nic innego, jak symboliczny zapis jakiejś reguły.
Umiecie również obliczać „wartość” wzoru, gdy znamy wartość liter występujących w tym wzorze. Dzisiaj nauczymy się sami takie wzory tworzyć.
Wzór możemy zapisać znając opis słowny.
Zapisz w zeszycie:

Wykonaj: zad. 2 i 3 ze str. 177 oraz 4 ze str. 178 w podręczniku.
ćw. 3 na str. 142 w zeszycie ćwiczeń.
Dla chętnych: zad. 5 i 7 ze str. 178 w podręczniku.
*Wersja do wydruku:Lekcja 38 – Korzystanie ze wzorów – ćwiczenia.
Lekcja 39
Temat: Plan, mapa, skala.
Cel lekcji: Nauczę się stosować różne sposoby zapisywania skali i obliczać rzeczywiste odległości na podstawie skali.
Z pojęciem skali spotkaliście się już w klasie czwartej. W skali przedstawiamy jakiś przedmiot, jeżeli chcemy go pomniejszyć lub powiększyć w stosunku do wymiarów rzeczywistych.
Skale typu: 1 : 2, 1 : 10, 1 : 25000 to skale pomniejszające. Skale typu: 2 : 1, 5 : 1 to skale powiększające.
Na planach i mapach używamy zawsze skali pomniejszającej. Na każdej mapie jest legenda, a w niej skala zapisana na trzy sposoby: jako skala liczbowa, mianowana i liniowa.
Przepisz do zeszytu:
Jeżeli korzystamy z mapy i chcemy obliczyć rzeczywistą odległość między dwoma punktami, musimy znać skalę mapy i odległość na mapie między tymi punktami.
Skala 1 : 500 oznacza, że 1 cm na mapie to 500 cm w rzeczywistości. Skala 1 : 25000 oznacza, że 1 cm na mapie odpowiada 25000 cm w rzeczywistości itd.
Skalę liczbową wygodnie zamienić na skalę mianowaną.
Zapisz w zeszycie:
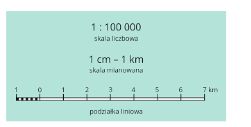
Jeżeli korzystamy z mapy i chcemy obliczyć rzeczywistą odległość między dwoma punktami, musimy znać skalę mapy i odległość na mapie między tymi punktami.
Skala 1 : 500 oznacza, że 1 cm na mapie to 500 cm w rzeczywistości. Skala 1 : 25000 oznacza, że 1 cm na mapie odpowiada 25000 cm w rzeczywistości itd.
Skalę liczbową wygodnie zamienić na skalę mianowaną.
Zapisz w zeszycie:
1 : 500 000
1 cm – 500 000 cm
1 cm – 5000 m
1 cm – 5 km
Jeżeli wiemy, że 1 cm na mapie to 5 km w rzeczywistości, to 2 cm na mapie to 2 · 5 km = 10 km w rzeczywistości.
Przeanalizuj przykład 2 na str. 183 w podręczniku.
Wykonaj: Przykłady a, b, c z poziomów B, C, D z zad. 1 ze str. 184 w podręczniku.
Dla chętnych: Poziom Mistrza z zad. 1 na str. 184 w podręczniku.
*Wersja do wydruku Lekcja 39 – Plan, mapa i skala
Tydzień obowiązywania: 1 – 5 czerwca 2020 r.
Lekcja 34
Temat: Prędkość, droga, czas – rozwiązywanie zadań.
Cel lekcji: Wykorzystam zdobyte umiejętności w sytuacjach praktycznych.
Na poprzedniej lekcji nauczyliście się obliczać: prędkość – gdy dana jest droga i czas, drogę – gdy dana jest prędkość i czas oraz czas – gdy dana jest droga i prędkość. Dzisiaj czas na wykorzystanie tych umiejętności w rozwiązywaniu konkretnych zadań. Przejrzyjcie dokładnie notatkę z ostatniej lekcji. Znajdziecie tam wszystkie typy zadań i sposób ich rozwiązania.
Wykonajcie samodzielnie: zad. 2, 4, 5, ze str. 165 w podręczniku oraz ćw. 6 na str. 139 w zeszycie ćwiczeń.
Dla chętnych: zad. 10 ze str. 165 w podręczniku.
*Wersja do wydruku Lekcja 34 – prędkość, droga, czas – rozwiązywanie zadań
Lekcja 35
Temat: Prędkość, droga, czas – cz. 2
Cel lekcji: Nauczę się rozwiązywać zadania dotyczące prędkości, w których występują ułamki.
Zadania, które rozwiązywaliśmy na poprzednich lekcjach, nie zawierały ułamków. Prędkość, droga i czas wyrażone były liczbami naturalnymi. Wiecie jednak, że podróż nie trwa dokładnie 2, 3 czy 5 godzin, ale np. 1 godz. 20 min lub 50 minut. Wtedy obliczenia są trochę bardziej złożone, bo najpierw trzeba zamienić jednostki. Dzisiaj będziemy zamieniać godziny na minuty i odwrotnie.
Przeanalizuj Przykład 1 ze str. 168 w podręczniku.
Zapisz w zeszycie:
Ile to minut?
Ile to godzin?
Wykonaj: przykłady a, b, c z poziomów A, B, C, D z zad. 1 ze str. 170 w podręczniku.
Dla chętnych: ćw. 2 i 3 na str. 140 w zeszycie ćwiczeń.
*Wersja do wydruku Lekcja 35 – prędkość, droga, czas – cz. 2
Lekcja 36
Temat: Prędkość, droga, czas – rozwiązywanie zadań tekstowych.
Cel lekcji: Utrwalę zdobyte umiejętności rozwiązując zadania tekstowe.
Na ostatniej lekcji nauczyliście się zamieniać minuty na godziny i odwrotnie. Tę umiejętność wykorzystamy dzisiaj w rozwiązywaniu zadań tekstowych.
Zadania rozwiązujemy tak, jak robiliśmy to wcześniej. Musimy jednak pamiętać, że jednostki używane w zadaniu muszą się zgadzać. Jeżeli prędkość wyrażona jest w km/h, to czas musi być wyrażony w godzinach. Jeżeli prędkość podana jest w m/min, to czas wyrażamy w minutach.
Przeanalizuj Przykłady 1- 5 na str. 169/170 w podręczniku. Są tam rozwiązane przykładowe zadania, które mogą być przydatne w wykonywaniu pracy samodzielnej.
Wykonaj: zad. 2 i 3 ze str. 171 oraz zad. I, II i III z „Czy już umiem?” ze str. 173 w podręczniku.
Dla chętnych: ćw. 4 na str. 141 w zeszycie ćwiczeń.
*Wersja do wydruku Lekcja 36 – Prędkość, droga, czas – zadania tekstowe
Lekcja 37
Temat: Korzystanie ze wzorów.
Cel lekcji: Nauczę się obliczać wartość wyrażenia dla podanych wartości.
Wzory nie są dla Was czymś nowym. Wykorzystywaliście je obliczając pola figur płaskich, objętość i powierzchnię brył, a także obliczając prędkość, drogę, czas.
Wzór, to nic innego, jak symboliczny zapis jakiejś reguły.
Umiecie obliczać „wartość” wzoru, gdy znamy wartość liter występujących w tym wzorze. Robiliście to obliczając pole powierzchni, objętość, prędkość.
Przepisz do zeszytu:
Zad.
Oblicz z dla x = 4, y = 8.
- a) z = 3x + 2y – 1
z = 3 · 4 + 2 · 8 – 1 = 12 + 16 – 1 = 27
- b) z = x² + 2,5y
z = 4² + 2,5 · 8 = 16 + 20 = 36
Wykonaj: przykłady a, b, c z poziomów A, B, C z zad. 1 ze str. 177 w podręczniku oraz ćw. 1 i 2 na str. 142 w zeszycie ćwiczeń.
Dla chętnych: Poziom Mistrza w zad. 1 ze str. 177 w podręczniku
*Wersja do wydruku Lekcja 37 – Korzystanie ze wzorów
Lekcja 30 Lekcja 31 Lekcja 32 Lekcja 33
Tydzień obowiązywania: 25 – 29 maja 2020 r.
Temat: Diagramy i wykresy – ćwiczenia.
Cel lekcji: Nauczę się wykorzystywać informacje z diagramów i wykresów.
Na poprzedniej lekcji nauczyliście się odczytywać informacje z diagramów oraz sporządzać diagramy słupkowe na podstawie podanych informacji. Dzisiaj będziemy odczytywać informacje z wykresów. Pamiętaj, żeby zwrócić szczególną uwagę na to, jak opisane są osie wykresu i jakie jednostki przyjęto. Przypomnij sobie, jak odczytujemy informacje z wykresów.
Zadania do wykonania:
Przeanalizuj raz jeszcze Przykład 2 ze strony 149 w podręczniku.
Wykonaj zad. 8 ze strony 153 w podręczniku oraz ćw. 6 na str. 132 w zeszycie ćwiczeń.
W zadaniach, które wykonaliście należało jedynie udzielić odpowiedzi na pytania odczytując informacje z wykresu. Dane z wykresu lub diagramu możemy wykorzystywać do rozwiązywania bardziej złożonych zadań.
Wykonaj ćw. 5 na str. 132 w zeszycie ćwiczeń.
Uważnie wypełnij tabelkę, która znajduje się w tym ćwiczeniu. Pamiętaj, że aby policzyć średnią kilku liczb należy je dodać, a otrzymaną sumę podzielić przez tyle, ile było liczb.
Dla chętnych:
Ćw. 4 na str. 131 w zeszycie ćwiczeń.
*Wersja do wydruku Lekcja 30 – Diagramy i wykresy – ćwiczenia
Temat: Procenty.
Cel lekcji: Nauczę się zamieniać procenty na ułamki i obliczać procent liczby.
Na pewno każdy z Was spotkał się w życiu codziennym z pojęciem procentu. W procentach podawane są obniżki cen, podatki, skład artykułów spożywczych i wiele innych. Procent to nic innego jak ułamek.
Możesz obejrzeć krótki filmik, który przybliży Ci pojęcie procentu.
https://www.youtube.com/watch?v=jeVSbsZ-AtI
Zapisz w zeszycie:
1% = 1% = 0,01 100% = 1
Procenty możemy zamienić na ułamek zwykły lub dziesiętny np.:
23% = = 0,23
117% = = 1= 1,17
Zapoznaj się z niebieską tablicą „Zapamiętaj” na str. 156 w podręczniku i przepisz jej zawartość do zeszytu.
Wykonaj ćw. 3 na str. 134 oraz ćw. 4 i 5 na str. 135 w zeszycie ćwiczeń.
Wykonaj zad. 2 i 3 ze str. 158 w podręczniku.
Dla chętnych:
Zad. 5 ze str. 159 w podręczniku.
*Wersja do wydruku Lekcja 31 – Procenty
Temat: Procenty – rozwiązywanie zadań.
Cel lekcji: Nauczę się wykorzystywać zdobyte umiejętności w rozwiązywaniu zadań tekstowych.
Na dzisiejszej lekcji będziemy rozwiązywać zadania tekstowe, w których wykorzystamy zdobytą dotychczas wiedzę o procentach. Pamiętamy, że całość to 100%.
Jeżeli wiemy, że morza i oceany zajmują 71% powierzchni Ziemi, to łatwo możemy obliczyć jaki procent powierzchni Ziemi zajmują lądy. Wystarczy wykonać działanie:
100% – 71% = 29%
Lądy zajmują zaledwie 29% powierzchni Ziemi.

Wykonaj zad. 4 ze str. 158 i zad. 9 ze str. 159 w podręczniku.
Dla chętnych:
Zad. 11 i 12 ze str. 160 w podręczniku.
Praca na ocenę.
Tym razem do wykonania na ocenę macie test. Linki do testu będą w dzienniku elektronicznym w pracy domowej z tej lekcji. Wpiszemy je w dniu, kiedy odbywa się ta lekcja w danej klasie. Dla każdej klasy będzie oddzielny link z innym terminem wykonania testu. Termin będzie podany przez nauczyciela w pracy domowej. Po terminie nie będzie możliwości wykonania testu.
* Wersja do wydruku Lekcja 32 – Procenty – rozwiązywanie zadań
Temat: Prędkość, droga, czas – część 1
Cel lekcji: Nauczę się zależności między drogą, czasem i prędkością i wykorzystam je w rozwiązywaniu zadań.
Z pojęciem prędkości na pewno spotkał się każdy z Was. Mówimy, że rowerzysta jedzie z prędkością 20 kilometrów na godzinę, to znaczy, że w ciągu godziny przejeżdża 20 kilometrów.
W skrócie prędkość rowerzysty możemy zapisać ![]()
gdzie km oznacza kilometr, a h oznacza godzinę.
Z pojęciem prędkości spotkasz się wkrótce na lekcjach fizyki. Warto więc już teraz zacząć używać właściwych symboli używanych do oznaczenia prędkości, drogi i czasu.
Do oznaczania tych wielkości używamy małych liter.
Zapisz w zeszycie:
s – droga v – prędkość t – czas
Żeby obliczyć prędkość, trzeba przebytą drogę podzielić przez czas.

Żeby obliczyć przebytą drogę, trzeba prędkość pomnożyć przez czas.
s = v · t
Zad. 2
Jaką drogę pokonał piechur, który szedł przez 2,5 godziny z prędkością 6 kilometrów na godzinę?
t = 2,5 h
v = 6 km/h
s = v · t
s = 6 km/h · 2,5 h
s = 15 km
Odp. Piechur pokonał 15 km.
Żeby obliczyć czas, trzeba drogę podzielić przez prędkość.

Powyższe trzy zadania to podstawowe typy zadań, z którymi się spotkasz w dzisiejszym temacie.
Wykonując samodzielnie zadania:
· wypisz dane,
· napisz wzór,
· podstaw do wzoru i oblicz,
· pamiętaj o jednostkach,
· napisz odpowiedź (tak, jak w przykładowych zadaniach).
Wykonaj przykłady a, b, c z poziomów: A, B, C w zad. 1 ze str. 164 w podręczniku.
Dla chętnych:
Ćw. 4 na str. 138 w zeszycie ćwiczeń.
*Wersja do wydruku Lekcja 33 – Prędkość, droga, czas – część 1
Lekcja 26 Lekcja 27 Lekcja 28 Lekcja 29
Tydzień obowiązywania: 18 – 22 maja 2020 r.
Lekcja 26
Temat: Pole powierzchni ostrosłupa.
Cel lekcji: Nauczę się obliczać powierzchnię ostrosłupa.
Potraficie obliczyć powierzchnię graniastosłupa. Dzisiaj nauczycie się obliczać powierzchnię ostrosłupa. Pamiętajmy, że ostrosłup ma tylko jedną podstawę, a jego ściany boczne są trójkątami. Oznaczenia Pc, Pp oraz Pb są aktualne w obliczaniu powierzchni ostrosłupa.
Zapisz w zeszycie:
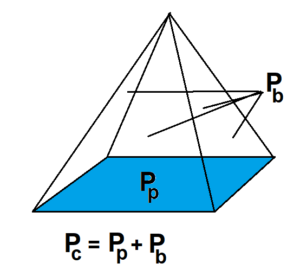
Pc – powierzchnia całkowita
Pp – pole podstawy
Pb – pole powierzchni bocznej (wszystkich ścian bocznych razem)
Zadanie
Oblicz powierzchnię całkowitą ostrosłupa, którego podstawą jest kwadrat o boku 6 cm, a wysokość ściany bocznej jest równa 12 cm.
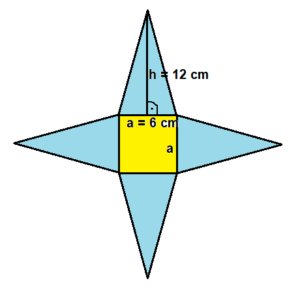
a = 6cm
hb = 12 cm (hb – wysokość ściany bocznej)
Pp = a · a
Pp = 6 cm · 6cm
Pp = 36 cm²
Pb = 4 · P trójkąta=4· 1/2 · a · h
Pb = 4 · 1/2 · 6 cm · 12 cm
Pb = 144 cm²
Pc = Pp + Pb
Pc = 36 cm² + 144 cm²
Pc = 180 cm²
Odp. Powierzchnia tego ostrosłupa jest równa 180 cm².
Samodzielnie wykonaj zad. 3b ze str. 132 w podręczniku oraz ćw. 3c na str. 123 i ćw. 6 na str. 126 w zeszycie ćwiczeń.
Wskazówka do ćw. 6: pamiętaj, że każdy romb jest równoległobokiem i jego pole możesz obliczać tak, jak pole równoległoboku.
Dla chętnych: zad. 13 ze str. 133 w podręczniku.
*Wersja do wydruku Lekcja 26 – Pole powierzchni ostrosłupa
Temat: Sprawdź, czy umiesz – siatki i powierzchnia brył.
Cel lekcji: Sprawdzę, czy dobrze opanowałem umiejętność rozpoznawania siatek i obliczania powierzchni brył.
Przyszedł czas na sprawdzenie, czego nauczyliście się o siatkach i powierzchni brył.
Przygotujcie kartkę w kratkę lub wydrukujcie treść zadań. Zadania dostępne są w pliku Praca nr 3 – siatki i powierzchnia brył (plik będzie udostępniony we wtorek).
Na górze kartki napiszcie: imię i nazwisko, klasa, poniżej: Praca nr 3 – siatki i powierzchnia brył.
Przeczytajcie uważnie polecenia i napiszcie rozwiązania zadań.
Po rozwiązaniu i sprawdzeniu swoich rozwiązań, kartkę włóżcie do przygotowanej specjalnie w tym celu teczki, koszulki, koperty lub w inne miejsce, gdzie będziecie gromadzić swoje prace.
Pracę należy przesłać swojej nauczycielce do sprawdzenia w terminie 2 dni roboczych od dnia, kiedy odbywa się ta lekcja za pomocą aplikacji Teams lub na maila.
Zwróćcie uwagę na to, by wasze rozwiązania zawierały następujące elementy:
1. Wypisane dane
2. Napisane wzory
3. Zapisane wszystkie obliczenia
4. Zapisane poprawne jednostki długości, pola
5. Napisaną odpowiedź.
Wersje pracy do pobrania:
WORD Praca nr 3 – Siatki i powierzchnia brył
PDF Praca nr 3 – siatki i powierzchnia brył
*Wersja do wydruku Lekcja 27 – Sprawdź, czy umiesz – siatki i powierzchnia brył
Temat: Tabele.
Cel lekcji: Nauczę się odczytywać informacje z tabeli i wykorzystywać je w rozwiązywaniu zadań.
Poszukując informacji w różnych sytuacjach z życia codziennego, korzystamy z różnorodnych źródeł. Jednym z takich źródeł są tabele. W tabelach zbierane są różne dane statystyczne dotyczące państw, społeczeństw itp.
Zadania do wykonania:
Przyjrzyjcie się tabeli „Kryta pływalnia” na str. 145 i rozwiążcie zadania 1 i 2 str. 145
A teraz przyjrzyjcie się tabeli „Polska i jej sąsiedzi” na stronie 142 w podręczniku. Będziecie z niej korzystać rozwiązując zadania z dzisiejszej lekcji.
Przeczytajcie Dobrą radę na stronie 143.
Zwracajcie uwagę na czytanie nagłówków tabeli, a szczególnie jednostek, w których zostały podane liczby w tabeli (przypomnijcie sobie, co oznaczają skróty: tys. i mln).
Wykonajcie zadania: 4 i 5 ze str. 145 w podręczniku.
Dla chętnych:
Ćw. 5 na stronie 128 w zeszycie ćwiczeń.
*Wersja do wydruku Lekcja 28 – Tabele
Temat: Diagramy i wykresy.
Cel lekcji: Nauczę się odczytywać informacje z wykresów i diagramów oraz sporządzać diagramy słupkowe.
Diagram to po prostu graficzne przedstawienie danych. Już wiecie, że informacje można przekazać w tekście oraz w tabeli. Czasami musimy porównać podane informacje i wtedy zrobimy to najszybciej korzystając z diagramu np. diagramu słupkowego.
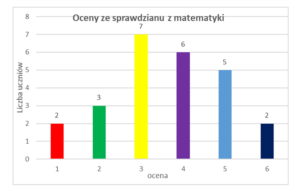
Wystarczy spojrzeć na powyższy wykres, żeby stwierdzić, że 7 osób (najwięcej) dostało trójkę ze sprawdzianu, 6 osób dostało czwórkę itd. Korzystając z tego diagramu możemy też obliczyć ile osób pisało sprawdzian, a także policzyć średnią ocen ze sprawdzianu. Zanim będziecie odczytywać informacje z diagramu, zwróćcie uwagę, jaki jest tytuł diagramu i jak opisane są osie.
Możesz obejrzeć filmik, który pokazuje na co trzeba zwrócić uwagę korzystając z diagramu. https://www.youtube.com/watch?v=msyy-WTr7Fc
Zadania do wykonania:
Przeanalizuj Przykład 1 i 2 ze strony 149 w podręczniku.
Wykonaj zad. 1 ze str. 151 w podręczniku.
Wykonaj ćw. 2/130 i ćw. 3/131 w zeszycie ćwiczeń.
Dla chętnych:
Zad. 3 ze str. 151 w podręczniku.
*Wersja do wydruku Lekcja 29 – Diagramy i wykresy
Tydzień obowiązywania: 11 – 15 maja 2020 r.
Lekcja 22
Temat: Siatki graniastosłupów i ostrosłupów – ćwiczenia.
Cel lekcji: Utrwalę wiadomości i umiejętności związane z siatkami brył.
Na poprzedniej lekcji nauczyliście się rozpoznawać bryły na podstawie ich siatek, a także odczytywać z siatki wymiary bryły. Dzisiaj w dalszym ciągu będziemy zajmować się siatkami i utrwalać zdobyte umiejętności.
Zadania do wykonania:
Przeanalizuj zadanie 4 ze str. 124 w podręczniku. Zanim to zrobisz, przypomnij sobie Dobrą radę ze str. 122 i sprawdź, czy siatki spełniają warunki tam podane. Nie zapisuj rozwiązania w zeszycie.
Rozwiąż zad. I, II i III z „Czy już umiem” ze str. 127 w podręczniku.
Wykonaj ćwiczenie 8 i 9 na str. 118 w zeszycie ćwiczeń.
Dla chętnych:
Ćwiczenie 10 na str. 119 w zeszycie ćwiczeń.
*Wersja do wydruku Lekcja 22 – Siatki graniastosłupów i ostrosłupów – ćwiczenia
Lekcja 23
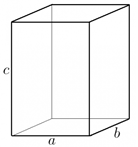
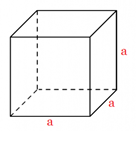
Temat: Pole powierzchni prostopadłościanu i sześcianu.
Cel lekcji: Nauczę się obliczać powierzchnię prostopadłościanów i sześcianów
Powierzchnia bryły to suma powierzchni wszystkich jej ścian. Jeżeli macie narysowaną siatkę bryły, to możecie policzyć powierzchnię każdej ściany, a następnie dodać otrzymane wyniki. Częściej jednak będziemy znali tylko wymiary bryły i na ich podstawie musimy umieć obliczyć powierzchnię całej bryły. Dzisiaj zajmiemy się obliczaniem powierzchni najbardziej znanych Wam brył, czyli prostopadłościanu i sześcianu.
Na początek obejrzyjcie dwa filmiki z epodręcznika.
https://epodreczniki.pl/a/pole-powierzchni-prostopadloscianu-i-szescianu/D68fHsGGS
Pamiętacie, że prostopadłościan ma trzy rodzaje ścian (po dwie ściany każdego rodzaju), a sześcian ma sześć identycznych ścian.
Zapiszcie w zeszycie:
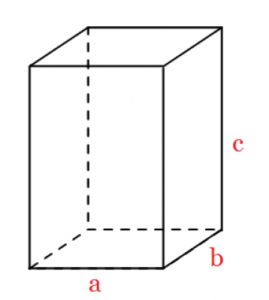
Pc – powierzchnia całkowita prostopadłościanu
Pc = 2 · a · b + 2 · b · c + 2 · a · c
Można zapisać krócej:
Pc = 2 · (a · b + b · c + a · c)
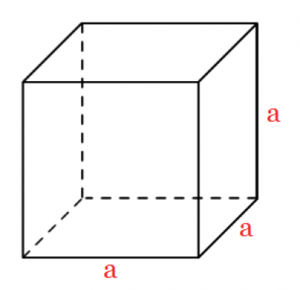
Pc = 6 · a · a
Można zapisać krócej:
Pc = 6 · a²
Przeanalizuj Przykład 1 na str. 129 w podręczniku.
Wykonaj zad. 1 ze str. 131 i zad. 2 ze str. 132 w podręczniku oraz ćwiczenie 2b, 2c na str. 122 w zeszycie ćwiczeń.
Uwaga:
- Rozwiązując zadanie wykonaj wszystkie czynności:
– wypisz dane
– napisz wzór
– podstaw do wzoru w miejsce liter odpowiednie wielkości
– oblicz
– napisz odpowiedź.
- Pamiętaj o używaniu odpowiednich jednostek.
Dla chętnych: ćw. 5 na str. 124 w zeszycie ćwiczeń.
*Wersja do wydruku Lekcja 23 – Pole powierzchni prostopadłościanu i sześcianu
Lekcja 24
Temat: Pole powierzchni graniastosłupa.
Cel lekcji: Nauczę się obliczać powierzchnię graniastosłupa.
Na poprzedniej lekcji obliczaliście powierzchnię prostopadłościanu i sześcianu. Dzisiaj nauczymy się obliczać powierzchnię innych graniastosłupów.
Pamiętacie, że każdy graniastosłup ma dwie identyczne (przystające) podstawy oraz prostokątne ściany boczne. Podstawą graniastosłupa może być dowolny wielokąt. Obliczając pole podstawy musimy zastosować właściwy wzór (tak, jak w przypadku obliczania objętości).
Zadania do wykonania:
Obejrzyj krótki filmik.
https://www.youtube.com/watch?v=4X4U8xkgZx0
Zapisz w zeszycie:

Uwaga: Pamiętaj, że pole powierzchni bocznej to pole wszystkich ścian bocznych razem.
Przeanalizuj Przykład 2 na stronie 130 w podręczniku.
Wykonaj zad. 3a ze str. 132 w podręczniku oraz ćw. 2a oraz 3a, 3b na str. 122 – 123 w zeszycie ćwiczeń.
Dla chętnych:
Zad. 11 ze str. 133 w podręczniku.
*Wersja do wydruku Lekcja 24 – Pole powierzchni graniastosłupa
Lekcja 25
Temat: Powierzchnia graniastosłupa – rozwiązywanie zadań.
Cel lekcji: Utrwalę umiejętność obliczania powierzchni graniastosłupa.
Dzisiaj utrwalimy umiejętność obliczania powierzchni graniastosłupów rozwiązując zadania tekstowe. Przypominam, że najbardziej „popularnymi” graniastosłupami są prostopadłościan i sześcian. Jeżeli ktoś nie będzie pamiętał wzorów na obliczanie objętości czy powierzchni prostopadłościanu lub sześcianu, może zastosować wzory na objętość i powierzchnię graniastosłupa.
Zadania do wykonania:
Zadanie 6 ze str. 132 w podręczniku.
Wskazówka: zastanów się, ile ścian ma akwarium?
Zadanie 8 i 12 ze str. 133 w podręczniku.
Wskazówka do zadania 12: możesz naszkicować sobie siatkę graniastosłupa (taką siatkę tylko z innymi wymiarami znajdziesz w zad. 6a/125).
Dla chętnych:
Zadanie 10 ze str. 133 w podręczniku.
*Wersja do wydruku Lekcja 25 – Powierzchnia graniastosłupa – rozwiązywanie zadań
Tydzień obowiązywania: 04 – 08 maja 2020 r.
Lekcja 18
Temat: Sprawdź, czy umiesz? – Graniastosłupy i ich objętość.
Cel lekcji: Sprawdzę czy umiem rozróżniać graniastosłupy i obliczać ich objętość.
1. Przygotujcie kartkę w kratkę lub wydrukujcie zadania.
2. Na górze kartki napiszcie: imię i nazwisko, klasa, poniżej:
Praca nr 2 – Graniastosłupy i ich objętość
3. Przeczytajcie uważnie polecenia i napiszcie rozwiązania poniższych zadań.
4. Po rozwiązaniu i sprawdzeniu swoich rozwiązań, kartkę włóżcie do przygotowanej specjalnie w tym celu teczki, koszulki, koperty lub w inne miejsce, gdzie będziecie gromadzić swoje prace.
5. Zdjęcie lub skan pracy prześlijcie swojej nauczycielce do sprawdzenia, najlepiej przez Zadania w Teamsie. Jeśli nie umiecie tego zrobić, to wyślijcie plik na maila podanego na początku strony.
6. Na odesłanie pracy macie 2 dni robocze od dnia, w którym przewidziana jest ta lekcja. Jeśli nie możecie odesłać pracy w tym terminie, to koniecznie skontaktujcie się ze swoją nauczycielką matematyki.
Praca nr 2 – Graniastosłupy i ich objętość (30 pkt)
Zad. 1 (4 pkt)
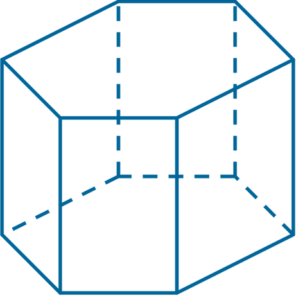
Nazwij ten graniastosłup. Napisz ile ma ścian, wierzchołków i krawędzi.
(nie rysuj go na kartce)
Zad. 2 (5 pkt)
Oblicz objętość prostopadłościanu o krawędziach: 16 cm; 4,5 cm; 0,8 dm.
Zad. 3 (5 pkt)
Oblicz objętość sześcianu o krawędzi 6 cm.
Zad. 4 (6 pkt)
Objętość prostopadłościanu jest równa 192 cm³. Dwie krawędzie mają długości 8 cm i 4 cm. Oblicz długość trzeciej krawędzi.
Zad. 5 (6 pkt)
Oblicz objętość graniastosłupa przedstawionego na rysunku:
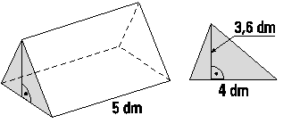
Zad. 6 (4 pkt)
Ala ma dzbanek w kształcie graniastosłupa o podstawie sześciokątnej, którego wysokość jest równa 15 cm. Do napełnienia tego dzbanka potrzeba 6 pełnych szklanek wody o pojemności 0, 35 l. Oblicz, ile centymetrów kwadratowych ma powierzchnia dna tego dzbanka.
Wersje pracy do pobrania:
WORD Praca nr 2 – graniastosłupy i ich objętość
PDF Praca nr 2 – graniastosłupy i ich objętość
*Wersja do wydruku Lekcja 18 – Sprawdź, czy umiesz – Graniastosłupy i ich objętość
Lekcja 19
Temat: Zamiana jednostek.
Cel lekcji: Nauczę się zamieniać jednostki długości, powierzchni i objętości.
Już w klasach młodszych poznaliście różne jednostki długości i związki między nimi.
Zapewne pamiętacie, że 1 m = 10 dm = 100 cm = 1000 mm. W przypadku jednostek powierzchni
i objętości te zależności są zupełnie inne. W kwadracie o boku 1 cm „zmieści się” aż 100 małych kwadracików o boku 1mm, a w sześcianie o krawędzi 1 cm „ zmieści się” aż 1000 małych sześcianików o krawędzi 1 mm.
Trudno to sobie wyobrazić. Pomogą wam w tym rysunki na stronie 115 w podręczniku. Przyjrzyjcie się im, a następnie przepiszcie do zeszytu informacje, które znajdują się pod rysunkami.
Zwróćcie uwagę na rzadziej używane jednostki powierzchni: ar (a) to powierzchnia kwadratu
o boku 10 m, a hektar (ha) to powierzchnia kwadratu o boku 100 m. Jest jeszcze większa jednostka powierzchni: km² – powierzchnia kwadratu o boku 1 km.
Na jednej z poprzednich lekcji używaliśmy litra (l) jako jednostki objętości.
Zapiszcie w zeszycie:
1 dm³ = 1 l
1 ³cm = 1 ml (mililitr)
1 l = 1000 ml
Zadania do wykonania:
Przeanalizujcie przykłady 1, 2 i 3 ze strony 116 – 117 w podręczniku, a następnie wykonajcie zad. 1 i 2 na str. 117 i zad. 6 ze str. 118 w podręczniku.
Dla chętnych:
Zad 8/ 118 z podręcznika.
*Wersja do wydruku Lekcja 19 – Zamiana jednostek
Lekcja 20
Temat: Siatki prostopadłościanów i sześcianów.
Cel lekcji: Nauczę się rysować siatki prostopadłościanów i sześcianów.
Zapewne pamiętacie, że mówiąc siatka bryły mamy na myśli figurę płaską, z której można zbudować bryłę. Siatki prostopadłościanów i sześcianów rysowaliście już w klasie piątej.
Dzisiaj przypomnimy sobie tę umiejętność. Na początek obejrzyjcie krótki filmik z epodręcznika: https://epodreczniki.pl/a/siatki-i-modele-prostopadloscianow-i-szescianow/D136DMxFq
Ciekawostka: istnieje 11 siatek sześcianu. Jeśli chcesz je wszystkie zobaczyć, poszukaj w Internecie.
Zadania do wykonania:
Narysuj siatkę:
a) prostopadłościanu o krawędziach 3 cm, 1 cm, 4 cm,
b) sześcianu o krawędzi 2,5 cm.
Oblicz objętości tych brył.
Wskazówki:
1. Sprawdź, czy Twoja siatka ma właściwą liczbę ścian.
2. Sprawdź, czy krawędzie, które się sklejają mają tę samą długość.
Wykonaj zadanie 1 ze strony 123 w podręczniku.
Dla chętnych:
Zadanie 7a ze strony 125 w podręczniku.
*Wersja do wydruku Lekcja 20 – Siatki prostopadłościanów i sześcianów
Lekcja 21
Temat: Siatki graniastosłupów i ostrosłupów.
Cel lekcji: Nauczę się rozpoznawać i rysować siatki graniastosłupów i ostrosłupów.
Potraficie już rozpoznawać i nazywać bryły. Dzisiaj nauczycie się rozpoznawać ich siatki.
Siatka graniastosłupa musi mieć dwie identyczne podstawy oraz ściany boczne, które są prostokątami. Siatka ostrosłupa ma jedną podstawę, a jej ściany boczne są trójkątami. To jest podstawowa różnica, która pozwoli Wam odróżniać siatki graniastosłupów i ostrosłupów.
Zapoznajcie się z krótkimi filmami z podręcznika.
https://epodreczniki.pl/a/siatki-i-modele-graniastoslupow/DuBZATbgg https://epodreczniki.pl/a/ostroslupy/D4UOCTysd
Zadania do wykonania:
Obejrzyjcie rysunki brył i ich siatek na stronie 122 w podręczniku i przeczytajcie uważnie Dobrą radę.
Wykonajcie zad. 2 ze strony 123 oraz zad. 3 ze strony 124 w podręczniku.
Wskazówka: Pamiętajcie, że nazwa graniastosłupa i ostrosłupa zależy od tego, jaki wielokąt jest jego podstawą.
Dla chętnych:
Wykonaj ćw. 4 i 5 na stronie 117 w zeszycie ćwiczeń.
*Wersja do wydruku Lekcja 21 – Siatki graniastosłupów i ostrosłupów
Tydzień obowiązywania: 27 – 30 kwietnia 2020 r.
Lekcja 15
Temat: Objętość prostopadłościanu.
Cel lekcji: Nauczę się obliczać objętość prostopadłościanu i sześcianu.
W klasie piątej nauczyliście się obliczać objętość prostopadłościanu i sześcianu. Poznaliście wzory na obliczanie objętości tych brył. Jeśli ktoś nie pamięta to przypomni sobie oglądając ten filmik: https://epodreczniki.pl/a/objetosc-prostopadloscianu/D1HufllvV
Przerysujcie i przepiszcie do zeszytu:
V – objętość
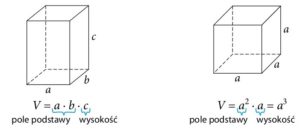
Zad. 1
Oblicz objętość prostopadłościanu o krawędziach 8 cm, 2 dm, 0,12 m.
a = 8 cm
b = 2 dm = 20 cm
c = 0,12 m = 12 cm
V = a · b · c
V = 8 cm · 20 cm · 12 cm
V = 1920 cm³
Odp. Objętość tego prostopadłościanu jest równa 1920 cm³.
Zad. 2
Oblicz objętość sześcianu o krawędzi 11 cm.
a = 11 cm
V = a · a · a
V = 11 cm · 11 cm · 11 cm
V = 1331 cm³
Odp. Objętość tego sześcianu jest równa 1331 cm³.
Uwagi:
1. Zadania wykonuj wg następujących zasad:
– wypisz dane
– napisz wzór
– podstaw do wzoru w miejsce liter odpowiednie liczby
– oblicz
– napisz odpowiedź
2. Jeżeli długości krawędzi wyrażone są w różnych jednostkach, zamień je na jeden rodzaj.
3. Pamiętaj, że objętość wyrażamy w jednostkach sześciennych (dokładniej zajmiemy się jednostkami na jednej z kolejnych lekcji).
A teraz wykonaj zad. 2
Zad. 2
Oblicz objętość:
a) prostopadłościanu o krawędziach: 13 cm, 0,08 m i 1,5 dm.
b) sześcianu o krawędzi 8 cm.
Czasami zadania są trochę bardziej złożone, ale jeżeli będziecie postępować zgodnie z zasadami, na pewno uda się Wam je rozwiązać.
Przepisz do zeszytu:
Zad. 3
Objętość prostopadłościanu jest równa 288 cm³. Oblicz wysokość tego prostopadłościanu, wiedząc, że długość jest równa 12 cm, a szerokość wynosi 8 cm.
V = 288 cm³
a = 12 cm
b = 8 cm
c = ?
V = a · b · c
288 cm³ = 12 cm · 8 cm · c
288 cm³ = 96 cm² · c
c = 288 cm³ : 96 cm²
c = 3 cm
Odp. Wysokość tego prostopadłościanu jest równa 3 cm.
Zad. 4
Objętość sześcianu jest równa 64 dm³. Oblicz jego krawędź.
V = 64 dm³
a = ?
V = a · a · a
64 dm³ = a · a · a
a = 4 dm
Odp. Krawędź tego sześcianu jest równa 4 dm.
Uwaga:
W przypadku obliczania krawędzi sześcianu nie można wykonać dzielenia. Trzeba odgadnąć, jaka liczba podniesiona do potęgi trzeciej (trzykrotnie pomnożona przez siebie) daje taki wynik.
A teraz wykonaj zad. 5 i 6.
Zad. 5
Dwie krawędzie prostopadłościanu o objętości 120 cm³ są równe 8 cm i 3 cm. Oblicz długość trzeciej krawędzi.
Zad. 6
Oblicz krawędź sześcianu, którego objętość jest równa 125 cm³.
*Wersja do wydruku Lekcja 15 – Objętość prostopadłościanu
Lekcja 16
Temat: Objętość graniastosłupa.
Cel lekcji: Nauczę się obliczać objętość graniastosłupa.
Na poprzedniej lekcji obliczaliście objętość prostopadłościanu i sześcianu. Wszyscy pamiętamy, że prostopadłościan i sześcian są także graniastosłupami.
Przyjrzyjmy się jeszcze raz wzorom na obliczanie objętości tych brył.
W prostopadłościanie:
V = a · b · c
a · b to pole podstawy prostopadłościanu, a c to jego wysokość.
Możemy zatem zapisać V = Pp · H, gdzie Pp – pole podstawy, H – wysokość
Podobnie w przypadku sześcianu:
V = a · a · a
a · a to pole podstawy sześcianu, a – to wysokość sześcianu.
Znowu możemy zapisać: V = Pp · H
W ten właśnie sposób możemy obliczyć objętość każdego graniastosłupa.
Obejrzyj jeszcze krótki filmik:
https://www.youtube.com/watch?v=S8HrnvYJBN8
Przerysuj do zeszytu i zapisz:
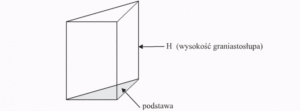
V = Pp · H
Pp – pole podstawy
H – wysokość graniastosłupa
Uwaga:
1. Podstawą graniastosłupa może być dowolny wielokąt, a zatem obliczając pole podstawy musisz wybrać odpowiedni wzór.
2. Wysokość graniastosłupa będziemy oznaczać wielką literą H, żeby nie myliła nam się z wysokością wielokąta, który będzie w podstawie.
Zapisz w zeszycie:
Zad.
Oblicz objętość graniastosłupa o wysokości 12 cm, którego podstawą jest równoległobok o podstawie 6 cm i wysokości 5 cm.
H = 12 cm
a = 6 cm
h = 5 cm
Pp = a · h
Pp = 6 cm · 5 cm
Pp = 30 cm²
V = Pp · H
V = 30 cm² · 12 cm
V = 360 cm³
Odp. Objętość graniastosłupa jest równa 360 cm³.
A teraz wykonaj zad. 4 ze str. 110 w podręczniku.
Dla chętnych: ćwicz. 6/112 w zeszycie ćwiczeń.
*Wersja do wydruku Lekcja 16 – Objętość graniastosłupa
Lekcja 17
Temat: Objętość graniastosłupa – ćwiczenia.
Cel lekcji: Utrwalę umiejętność obliczania objętości graniastosłupa.
Na ostatniej lekcji poznaliście wzór na obliczanie objętości graniastosłupa i rozwiązaliście pierwsze zadania. Dzisiaj także będziemy obliczać objętość graniastosłupa.
Zadana do wykonania:
Zanim rozwiążesz następne zadanie zapisz i zapamiętaj:
1 litr = 1 dm³
Rozwiąż zad. 3/110 z podręcznika.
Wskazówki do zad. 3
1. Jeśli chcesz otrzymać wynik w litrach, czyli w dm³, zamień wymiary basenu na dm
(1m = 10 dm).
2. Aby obliczyć ułamek liczby, trzeba pomnożyć ułamek przez tę liczbę.
Rozwiąż zad. I, II i III z „Czy już umiem?” z podręcznika ze str. 113.
Dla chętnych: ćw. 7/113 w zeszycie ćwiczeń.
*Wersja do wydruku Lekcja 17 – Objętosć graniastosłupa – ćwiczenia
Tydzień obowiązywania: 20 – 24 kwietnia 2020 r.
Lekcja 11
Temat: Rozwiązywanie zadań tekstowych.
Cel lekcji: Utrwalę umiejętność wykorzystania równań w rozwiązywaniu zadań tekstowych.
Na ostatniej lekcji przekonaliście się, jak prosto można rozwiązać zadanie tekstowe, jeżeli zastosujemy w tym rozwiązaniu równanie. Trzeba je tylko prawidłowo ułożyć, a potem rozwiązać i sprawdzić poprawność swojego rozwiązania. Zawsze dokładnie czytaj treść zadania. Niekiedy wydaje się niemal taka sama, a jednak rozwiązanie jest zupełnie inne.
Zadania do wykonania
1. Zapiszcie w zeszycie:
Zad. 1
Ania i Kasia mają razem 48 płyt z muzyką. Kasia ma o 2 płyty więcej niż Ania. Ile płyt ma Ania, a ile Kasia?
x – płyty Ani
x + 2 – płyty Kasi
x + x + 2 = 48
2x + 2 = 48/-2
2x = 46/:2
x = 23 – płyty Ani
x + 2 = 23 + 2 = 25 – płyty Kasi
spr. 23 + 25 = 48 razem
Odp. Ania ma 23 płyty, a Kasia 25 płyt.
Zad. 2
Ania i Kasia mają razem 48 płyt z muzyką. Kasia ma 2 razy więcej płyt niż Ania. Ile płyt ma Ania, a ile Kasia?
x – płyty Ani
2x – płyty Kasi
x + 2x = 48
3x = 48/:3
x = 16 – płyty Ani
2x = 2 · 16 = 32 – płyty Kasi
spr. 16 + 32 = 48 razem
Odp. Ania ma 16 płyt, a Kasia 32 płyty.
2. Rozwiążcie teraz zadanie 5 i 6 ze str. 97 w podręczniku.
Czasami, przed rozwiązaniem zadania, warto wykonać rysunek pomocniczy. Taki rysunek pomoże nam wyobrazić sobie sytuację przedstawioną w zadaniu. Przypomnijcie sobie z poprzedniej lekcji przykład 1 ze str. 94 w podręczniku.
3. Wykonajcie teraz zadanie 8 ze str. 97 w podręczniku.
Dla chętnych:
Jeśli chcecie poćwiczyć dodatkowo wykonajcie ćw.6/106 i ćw. 7/107 w zeszycie ćwiczeń.
*Wersja do wydruku Lekcja 11 – Rozwiazywanie zadań tekstowych
Lekcja 12
Temat: Równania – powtórzenie.
Cel lekcji: Powtórzę i utrwalę umiejętność rozwiązywania równań oraz wykorzystywania równań w rozwiązywaniu zadań tekstowych.
Uczyliście się sprawdzać, czy dana liczba jest rozwiązaniem równania, upraszczać równanie, rozwiązywać równanie oraz wykorzystywać równania w rozwiązywaniu zadań tekstowych. Dzisiaj utrwalicie sobie te umiejętności rozwiązując zadania powtórzeniowe z podręcznika. Jeżeli nie będziecie czegoś pamiętali, zajrzyjcie do swoich notatek lub do podręcznika. Ale przede wszystkim pamiętajcie, że Wasi nauczyciele matematyki służą Wam pomocą podczas lekcji.
Zadania do wykonania
Wykonajcie zadania 1, 2, 3, 4 i 7 ze str. 100 w podręczniku.
Dla chętnych:
Jeśli chcesz poćwiczyć dodatkowo wykonaj w zeszycie ćwiczeń ćwicz. 2 i 4/109 oraz ćw. 8, 9/110.
*Wersja do wydruku lekcja 12 – Równania – powtórzenie
Lekcja 13
Temat: Sprawdź, czy umiesz – równania.
Cel lekcji: Sprawdzę, czy umiem rozwiązywać równania i czy potrafię je wykorzystywać w rozwiązywaniu zadań tekstowych.
Przyszedł czas, aby sprawdzić czego nauczyliście się przez ostatnich kilka lekcji.
Przygotujcie kartkę w kratkę lub wydrukujcie treść zadań.
Na górze kartki napiszcie: imię i nazwisko, klasa, poniżej Sprawdzian nr 5 – Równania
Przeczytajcie uważnie polecenia i napiszcie rozwiązania poniższych zadań.
Pamiętaj, że rozwiązanie zadania tekstowego składa się z 6 “kroków”. Jeżeli któreś pominiesz, stracisz punkty.
Po rozwiązaniu i sprawdzeniu swoich rozwiązań, zróbcie zdjęcie pracy i wyślijcie swojej nauczycielce matematyki (pocztą elektroniczną lub przez aplikację Teams).
Dodatkowo kartkę z pracą włóżcie do przygotowanej specjalnie w tym celu teczki, koszulki, koperty lub w inne miejsce, gdzie będziecie gromadzić swoje prace.
Jeśli nie możecie wysłać pracy lub wykonać jej w terminie, to skontaktujcie się ze swoją nauczycielką matematyki.
Termin odesłania – najpóźniej do poniedziałku 27 kwietnia do godz. 20.00
Sprawdzian nr 5 – Równania (max. 50 pkt)
Zadanie 1 (8 pkt)
Sprawdź, czy rozwiązaniem równania 4 · x – 7 = 19 jest podana liczba. Napisz TAK lub NIE. (pamiętaj o zapisaniu swoich obliczeń)
a) liczba 9
b) liczba 6,5
Zadanie 2 (9 pkt)
Rozwiąż równanie.
a) x : 9 = 16
b) 3 · x – 14 = 25
c) 7 · x – 2 + 4 · x = 42
Zadanie 3 (6 pkt)
Rozwiąż zadanie za pomocą równania.
Szklanka soku i porcja naleśników kosztują razem 17 zł, przy czym naleśniki są o 3 zł droższe od soku. Ile kosztuje szklanka soku, a ile naleśniki?
Zadanie 4 (7 pkt)
Wykonaj rysunek pomocniczy i zapisz na nim informacje podane w zadaniu. Rozwiąż
zadanie za pomocą równania.
Obwód trójkąta równoramiennego jest równy 42cm. Ramię jest 3 razy dłuższe od
podstawy. Oblicz długość podstawy.
Zadanie 5 (6 pkt)
Rozwiąż zadanie za pomocą równania.
Za cztery batoniki i jedną czekoladę Radek zapłacił 14 zł. Czekolada jest trzy razy droższa
od batonika. Ile kosztuje czekolada?
Zadanie 6 (8 pkt)
Rozwiąż równanie.
a) 13 · x – 8 = 6 · x + 20
b) 5 · x + 10 = 8 · x + 19
Zadanie 7 (6 pkt)
Rozwiąż zadanie za pomocą równania.
Dzbanek i kubek kosztują razem 72 zł. Gdyby dzbanek potaniał o 8 zł kosztowałby
trzykrotnie więcej niż kubek. Ile kosztuje kubek?
*Wersja do wydruku Lekcja 13 – Sprawdź, czy umiesz – równania
Lekcja 14
Temat: Bryły.
Cel lekcji: Nauczę się rozpoznawać i nazywać różne bryły oraz obliczać liczbę ścian, wierzchołków i krawędzi w tych bryłach.
W klasie czwartej poznaliście pierwsze bryły, czyli figury przestrzenne: prostopadłościan i sześcian.
W klasie piątej nauczyliście się rozpoznawać graniastosłupy i ostrosłupy.
Zadania do wykonania
Przypomnijcie sobie wiadomości o prostopadłościanach, sześcianach, graniastosłupach i ostrosłupach zamieszczone w epodręczniku.
https://epodreczniki.pl/a/szesciany-i-prostopadlosciany/D1BhAYGYE
https://epodreczniki.pl/a/graniastoslup-prosty/D1CSBwMzJ
https://epodreczniki.pl/a/ostroslup-i-jego-wlasnosci/Do5PUpIu1
Przerysujcie do zeszytu:
 |  |
| Prostopadłościan to bryła, której wszystkie ściany są prostokątami | Sześcian to prostopadłościan, który ma wszystkie krawędzie równe |
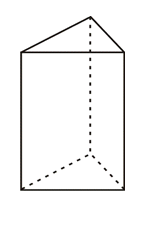 | 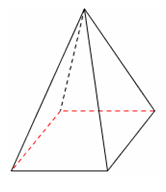 |
| Graniastosłup prosty to bryła, która ma dwie jednakowe podstawy będące wielokątami, a jej ściany boczne są prostokątami | Ostrosłup to bryła, której podstawą jest dowolny wielokąt, a ściany boczne są trójkątami o wspólnym wierzchołku |
Nazwa graniastosłupa i ostrosłupa oraz liczba jego ścian, wierzchołków i krawędzi zależy od wielokąta, który jest podstawą danej bryły.
Przyjrzyj się dokładnie rysunkom brył na stronie 106 w podręczniku.
Przerysuj tabelkę i uzupełnij ją według wzoru:
Nr bryły | Nazwa bryły | Liczba ścian | Liczba wierzchołków | Liczba krawędzi |
| 1 | ostrosłup sześciokątny | 7 | 7 | 12 |
| 2 | ||||
| 3 | ||||
| 4 | ||||
| 5 | ||||
| 6 | ||||
| 7 | ||||
| 8 | ||||
| 9 |
Dla chętnych:
Jeśli chcesz poćwiczyć dodatkowo, wykonaj ćw. 1/111 oraz ćw. 4 i 5/112.
*Wersja do wydruku Lekcja 14 – Bryły
Tydzień obowiązywania: 15 – 17 kwietnia 2020 r.
Lekcja 9
Temat: Trudniejsze równania.
Cel i opis lekcji: Będę doskonalić umiejętność rozwiązywania równań.
Na poprzedniej lekcji rozwiązywaliście trochę trudniejsze równania, w których trzeba było najpierw uprościć jedną stronę równania (poziom A) i w których niewiadome były też po prawej stronie równania (poziom B).
Na tej lekcji wykorzystamy te dwie umiejętności do rozwiązywania równań.
Zadania do wykonania:
- Najpierw przeanalizujcie w podręczniku na stronach 88 i 89 przykłady z poziomu C i D (czytajcie uważnie wyjaśnienia, które są obok przykładów).
- Zapiszcie w zeszycie przykład:
2x – 8 – 5x + 6 = 5 – 4x + 8x +7 upraszczamy lewą i prawą stronę równania
– 3x – 2 = 12 + 4x / – 4x odejmujemy 4x, żeby z prawej strony nie było niewiadomej
– 7x – 2 = 12 / + 2 dodajemy 2, żeby z lewej strony nie było liczb
– 7x = 14 /: (– 7) dzielimy przez (-7), czyli przez współczynnik przy x
x = – 2
- Wykonajcie w zeszycie zad. 1 str. 90 (z poziomu C i D przykłady a, b, c, d) z podręcznika.
Dla chętnych:
Jeśli chcecie jeszcze poćwiczyć rozwiązywanie równań, to rozwiążcie ćwiczenia: 5, 6 str. 102 oraz 7 str. 103 z zeszytu ćwiczeń.
*Wersja do wydruku Lekcja 9 – trudniejsze równania
Lekcja 10
Temat: Jak rozwiązać zadanie tekstowe?
Cel i opis lekcji: Nauczę się wykorzystywać równania do rozwiązywania zadań tekstowych.
Przez ostatnie lekcje uczyliście się, jak rozwiązywać równania. Teraz zobaczycie, jak bardzo ułatwiają one rozwiązywanie zadań tekstowych.
Zadania do wykonania:
1. Przeczytajcie i przeanalizujcie z podręcznika przykład 1. ze str. 94 oraz przykład 2. ze str. 95.
Czy zauważyliście, że poprawne rozwiązanie zadania tekstowego za pomocą równań składa się z kilku etapów? Muszą one znaleźć się w waszym rozwiązaniu, bo za każdy etap otrzymujecie punkty.
2. Zapiszcie w zeszycie schemat rozwiązywania zadania tekstowego, który znajduje się w podręczniku na górze strony 95.
3. Zanim zaczniecie rozwiązywać zadania tekstowe, nauczycie się sprawdzać, czy wasze rozwiązanie jest poprawne.
Wykonajcie zadania 1 i 2 str. 96 z podręcznika.
Do zadania 2. możecie zrobić i uzupełnić tabelkę taką, jak ta poniżej:
| Odp. | Lasse | Bosse | Olle | Razem | Powinno być | Czy poprawnie? |
| A | 80 | 80:2=40 | 80−50=30 | 80+40+30=150 | 250 | NIE |
| B | ||||||
| C | ||||||
| D |
4. A teraz zgodnie ze wskazówkami wykonajcie zadanie 3 ze strony 97 w podręczniku.
Dla chętnych
Jeśli chcecie jeszcze poćwiczyć, to możecie rozwiązać z zeszytu ćwiczeń następujące ćwiczenia:
1/104, 3, 4/105, 5/106
*Wersja do wydruku Lekcja 10 – rozwiazywanie zadań tekstowych za pomoca równań
Tydzień obowiązywania: 06 – 08 kwietnia 2020 r.
Lekcja 7
Temat: Równania – sprawdź, czy umiesz.
Cel lekcji: Sprawdzę czy potrafię rozwiązać proste równanie.
Przyszedł czas na sprawdzenie, czego nauczyliście się przez ostatnie lekcje.
Przygotujcie kartkę w kratkę.
Na górze kartki napiszcie: imię i nazwisko, klasa, poniżej Praca nr 1.
Przeczytajcie uważnie polecenia i napiszcie rozwiązania poniższych zadań.
Po rozwiązaniu i sprawdzeniu swoich rozwiązań, kartkę włóżcie do przygotowanej specjalnie w tym celu teczki, koszulki, koperty lub w inne miejsce, gdzie będziecie gromadzić swoje prace. Sprawdzimy je po powrocie do szkoły.
Oprócz tego, jeśli chcecie, możecie przesłać zdjęcie pracy do sprawdzenia.
Jeśli potraficie lub potrafią to wasi rodzice, to starajcie się, by wielkość pliku nie była za duża.
Zadania do wykonania:
Wykonaj podane zadania:
Zadanie 1.
Sprawdź, czy rozwiązaniem równania 8 · x – 9 = 11 jest podana liczba. Podkreśl TAK lub NIE.
a. x = 3 L =______________ P=___________ TAK NIE
b. x = 2,5 L= ______________ P=___________ TAK NIE
Zadanie 2.
Ułóż równanie do zadania:
Kasia pomyślała o pewnej liczbie. Pomnożyła ją przez 3, a do wyniku dodała 12 i otrzymała 90.
O jakiej liczbie pomyślała Kasia?
Uwaga: Nie zapomnij napisać co oznacza Twoja niewiadoma, nie rozwiązuj tego równania, tylko je ułóż.
Zadanie 3.
Rozwiąż równanie.
a) a + 17 = 54 d) d ∙ 8 = 112
_________________ _________________
_________________ _________________
b) 96 : b = 4 e) e : 7 = 13
_________________ _________________
_________________ _________________
c) 4c − 7 = 29 f) 6x + 12 = 36
_________________ _________________
_________________ _________________
Zadanie 4
Podaj wszystkie cztery rozwiązania równania x ∙ (x + 5)(x² – 36) = 0
*Wersja do wydruku Lekcja 7 – Równania – sprawdź czy umiesz
Lekcja 8
Temat: Trudniejsze równania.
Cel i opis lekcji: Nauczę się rozwiązywać trudniejsze równania.
Umiecie już rozwiązywać proste równania i sprawdzać, czy otrzymane rozwiązanie spełnia dane równanie Dzisiaj nauczymy się rozwiązywać trudniejsze równania, które przed rozwiązaniem będą wymagały uproszczenia.
Zadania do wykonania:
Przeanalizuj upraszczanie równań na stronie 86 w Twoim podręczniku i zapamiętaj „Dobrą radę”
ze strony 88.
Zapisz w zeszycie:
Zanim rozwiążesz równanie, uprość je, np.:
5x + 10 – 3x + 6 = 24
2x + 16 = 24/ -16
2x = 8/:2
x = 4
Sprawdź swoje rozwiązanie:
L = 5·4 + 10 – 3·4 + 6 = 20 + 10 – 12 + 6 = 30 – 12 + 6 = 18 + 6 = 24
P = 24
L = P
x = 4 jest rozwiązaniem równania.
Następnie przeanalizuj przykład 1 z poziomu B i C na stronie 88 (czytaj uważnie wyjaśnienia, które są obok przykładów). Możesz też obejrzeć krótki film: https://www.youtube.com/watch?v=NiEvoOaal8c
Wykonaj w zeszycie zad. 1 str. 90 (z poziomu A i B przykłady a, b, c, d).
Dla chętnych: zad. 5 str. 91 z podręcznika; ćw. 3 str.101 i ćw. 4 str. 102 w zeszycie ćwiczeń.
*Wersja do wydruku Lekcja 8 – Trudniejsze równania
Tydzień obowiązywania: 30 marca – 03 kwietnia 2020 r.
Lekcja 3
Temat: Równania, czyli skąd my to znamy.
Cel i opis lekcji: Nauczę się układać równania do prostych zadań tekstowych.
Na lekcji nauczysz się rozpoznawać równania z jedną niewiadomą, wskazywać lewą i prawą stronę równania oraz samodzielnie układać równania do zadań tekstowych.
Zapisz w zeszycie:
Wyrażenie typu 4 ∙ x + 7 = 19 nazywamy równaniem.
Literę x nazywamy niewiadomą.
W każdym równaniu występuje znak =, który oddziela lewą stronę równania od prawej strony równania.
L = 4 ∙ x + 7 (lewa strona) P = 19 (prawa strona)
Lewa strona = prawa strona
Równania bardzo często wykorzystujemy do rozwiązywania zadań tekstowych.
Uwaga:
Niewiadomą możemy oznaczać dowolną literą np.: b, d, t, y, z itp.
Zapis: 4 ∙ x można zastąpić zapisem 4x
Zadania do wykonania:
Najpierw przeanalizuj przykład 1 i 2 na stronie 68 w podręczniku.
Następnie wykonaj: zad. 1 i 2 ze str.69 z podręcznika.
Wskazówka do zad. 2: gdy wybierzesz niewiadomą ustal, co ona będzie oznaczać.
Materiały:
Jeżeli chcesz jeszcze lepiej przygotować się do rozwiązywania zadań zajrzyj do epodręcznika: https://epodreczniki.pl/a/zapisywanie-tresci-prostych-zadan-za-pomoca-rownan/DVqPleFEW
Jeśli Twój podręcznik został w szkole, możesz skorzystać z podręcznika w wersji on-line dostępnego bezpłatnie na platformie https://ebooki.nowaera.pl
Dla chętnych:
Jeśli chcesz poćwiczyć dodatkowo, możesz wykonać
zad. 4 ze str.70 w podręczniku oraz ćwiczenia 4 i 5 str. 94 z zeszytu ćwiczeń.
*Wersja do wydruku Lekcja 3 – Równania, czyli skąd my to znamy
Lekcja 4
Temat: Sprawdzanie, czyli rozwiązanie bez rozwiązywania.
Cel i opis lekcji: Nauczę się sprawdzać, czy dana liczba jest rozwiązaniem równania.
Na lekcji nauczysz się sprawdzać, czy podana liczba spełnia dane równanie.
Zapisz w zeszycie:
Liczba 3 jest rozwiązaniem równania 4 ∙ x + 7 = 19.
Mówimy wtedy, że liczba 3 spełnia to równanie.
Rozwiązać równanie, to znaczy znaleźć wszystkie liczby spełniające to równanie.
Równanie może mieć jedno, kilka lub nieskończenie wiele rozwiązań. Może też nie mieć żadnego rozwiązania.
Uwaga:
Żeby stwierdzić, czy dana liczba jest rozwiązaniem równania, należy wstawić w miejsce niewiadomej podaną liczbę i sprawdzić czy lewa strona równania równa jest prawej.
Na stronie 73 w podręczniku masz podane przykłady różnych równań. Obejrzyj je.
Zadania do wykonania:
Najpierw przeanalizuj przykład 1 na stronie 74 w podręczniku.
Następnie wykonaj: Zad 1 str. 75 Poziom A: a, b, c oraz poziom C: a, b, c.
Materiały:
Jeżeli chcesz jeszcze lepiej przygotować się do rozwiązywania zadań obejrzyj krótki film: https://www.youtube.com/watch?v=hMDZCis-F3Q
Jeśli Twój podręcznik został w szkole, możesz skorzystać z podręcznika w wersji on-line dostępnego bezpłatnie na platformie https://ebooki.nowaera.pl
Dla chętnych:
Jeśli chcesz poćwiczyć dodatkowo, możesz wykonać:
ćwiczenia 1, 2, 4 str. 96 z zeszytu ćwiczeń oraz zad. 11a ze str.77 w podręczniku.
*Wersja do wydruku Lekcja 4 – Sprawdzanie, czyli rozwiązanie bez rozwiązywania
Lekcja 5
Temat: Jak rozwiązać równanie.
Cel i opis lekcji: Nauczę się rozwiązywać proste równania.
Często porównuje się równania do wagi szalkowej. Co to jest waga szalkowa i co wspólnego ma
z równaniami przekonasz się oglądając krótki film:
https://epodreczniki.pl/a/film/D6TceWZyr
Zapisz w zeszycie:
Do obu stron równania można dodać tę samą liczbę lub od obu stron równania można odjąć tę samą liczbę np.:
5x + 4 = 29 / – 4 3x – 4 = 11 / +4
5x = 25 3x = 15
Obie strony równania możemy pomnożyć lub podzielić przez tę samą liczbę różną od 0 np.:
6x = 24 / :6 0,5x = 4 / ∙ 2
x = 4 x = 8
Zadania do wykonania:
Najpierw przeanalizuj przykład 1 na stronie 81 w podręczniku oraz Dobrą radę.
Następnie wykonaj: Zad 1 str. 82 Poziom A:a,b,c oraz poziom B:a,b,c.
Materiały:
Jeśli chcesz dodatkowo poćwiczyć, możesz to zrobić z epodręcznikiem: https://epodreczniki.pl/a/rozwiazywanie-rownan/DcDkqLKBI
Jeśli Twój podręcznik został w szkole, możesz skorzystać z podręcznika w wersji on-line dostępnego bezpłatnie na platformie https://ebooki.nowaera.pl
Dla chętnych:
Jeśli chcesz, możesz wykonać: ćwiczenie 1 str. 98 z zeszytu ćwiczeń, zad. 4 ze str.83 w podręczniku.
*Wersja do wydruku Lekcja 5 – Jak rozwiązać równanie
Lekcja 6
Temat: Jak rozwiązać równanie? – ćwiczenia.
Cel i opis lekcji: Utrwalę umiejętność rozwiązywania prostych równań.
Mam nadzieję, że udało Ci się rozwiązać równania z poprzedniej lekcji. Rozwiązywaliśmy je metodą działań odwrotnych. Jeśli do naszej niewiadomej ktoś dodał jakąś liczbę, to my odejmowaliśmy tę liczbę, oczywiście od obu stron równania. Jeśli ktoś odjął liczbę – my dodawaliśmy tę liczbę, jeśli ktoś pomnożył przez jakąś liczbę – my dzieliliśmy obie strony równania przez tę liczbę.
Dzisiaj równania będą trochę trudniejsze, ale poznane zasady stosujemy tak samo.
Przypominam, że zapisy 2∙x oraz 2x są równoważne (czyli oznaczają to samo);
Zapisz w zeszycie:
a) 3x + 2 = 11 /-2 b) 5x – 7 = 28 /+7 c) 1,5x + 4 = 7 /-4
3x = 9 /:3 5x = 35 /:5 1,5x = 3 /∙ 2
x = 3 x = 7 3x = 6 /:3
x = 2
Zadania do wykonania:
Zanim zaczniesz pracować samodzielnie, obejrzyj krótki filmik i przeanalizuj przykład Poziom C
na stronie 82 w podręczniku. https://www.youtube.com/watch?v=qdWyk3h6kF0
Następnie wykonaj: Zad 1 str. 82 Poziom C: a,b,c,g,h,i.
Materiały:
Jeśli chcesz dodatkowo poćwiczyć, możesz to zrobić z epodręcznikiem: https://epodreczniki.pl/a/rozwiazywanie-rownan/DcDkqLKBI
Jeśli Twój podręcznik został w szkole, możesz skorzystać z podręcznika w wersji on-line dostępnego bezpłatnie na platformie https://ebooki.nowaera.pl
Dla chętnych:
Jeśli chcesz, możesz wykonać: ćwiczenie 2 str. 99 oraz ćw. 5 str. 100 z zeszytu ćwiczeń, zad. 7
ze str.83 w podręczniku.
*Wersja do wydruku Lekcja 6 – Jak rozwiązać równanie – ćwiczenia
Tydzień obowiązywania: 25 – 27 marca 2020 r.
Lekcja 1.
Temat: Figury na kratce.
Cel i opis lekcji: Nauczę się wykorzystywać kratki do rysowania wielokątów
o danych wymiarach i odczytywać wymiary wielokątów
z rysunku.
Na lekcji nauczysz się, jak rysować znane Ci wielokąty o podanych wymiarach, nie używając linijki do mierzenia, a jedynie do narysowania prostych odcinków. Nauczysz się też odczytywać (nie mierzyć) długości odcinków narysowanego wielokąta, aby obliczyć jego powierzchnię.
Wskazówka:
Pamiętaj, że rysując wielokąt musisz umieścić jego wierzchołki w punkcie przecięcia kratek, a długości odcinków możesz odczytać tylko wtedy, gdy biegną one wzdłuż kratek, a nie ukośnie do nich.
Zadania do wykonania:
Najpierw przeanalizuj rysunki na str. 49 z podręcznika oraz przykład 1 na str. 50 i 2 na str. 51 w podręczniku.
Następnie wykonaj: zad. 1 str. 53 z podręcznika oraz ćwiczenie 10 na str.90 z zeszytu ćwiczeń.
Materiały:
Jeśli nie pamiętasz własności albo wzoru na pole czworokąta, możesz je sobie przypomnieć zaglądając do notatek, podręcznika lub e podręcznika.
https://epodreczniki.pl/a/obliczanie-pol-i-obwodow-czworokatow/DcfpefmJk
Jeśli Twój podręcznik został w szkole, możesz skorzystać z podręcznika w wersji on-line dostępnego bezpłatnie na platformie https://ebooki.nowaera.pl
Dla chętnych:
Jeśli chcesz poćwiczyć dodatkowo, możesz wykonać ćw. 11 ze str. 91 w zeszycie ćwiczeń.
Lekcja 2.
Temat: Figury płaskie – powtórzenie.
Cel i opis lekcji: Powtórzę i utrwalę wiadomości i umiejętności dotyczące wielokątów.
Zadania do wykonania:
Ostatnio wykonywaliście prace domowe, w których obliczaliście brakujące kąty wielokątów oraz obliczaliście ich pole powierzchni. Kolejny raz macie okazję sprawdzić swoje umiejętności rozwiązując zadania powtórzeniowe z podręcznika.
Wykonaj w zeszycie zad. 4, 6 i 7 ze strony 57 w podręczniku.
Jeśli nie masz w domu podręcznika możesz skorzystać z podręcznika w wersji on-line dostępnego bezpłatnie na platformie https://ebooki.nowaera.pl
Dla chętnych:
Ci z Was, którzy chcą zostać mistrzami matematyki, mogą dodatkowo poćwiczyć rozwiązując zadania z e podręcznika.
https://epodreczniki.pl/a/trening-mistrza—cwiczenia-przed-sprawdzianem/Df1Do5lg6
*Wersja do wydruku – Lekcja 1 i 2
Sprawdź, czy umiesz!
Zachęcamy do wykonania zadań. Rozwiązania zapisujcie na kartkach. Możecie przesyłać rozwiązane zadania (zeskanowane lub zrobione zdjęcie) jako załączniki na adres swoich nauczycielek:
Mirosława Modzelewska miroslawa_mm@op.pl
Anna Nowak anna.nowak04@gmail.com
Jolanta Skolimowska jolanta.skolimowska@wp.pl
Anna Wilk mmatematyczny@gmail.com
Sprawdzimy Wasze prace i wstawimy oceny. Tą drogą możecie też zadawać nam pytania.
Prosimy, pamiętajcie o podpisaniu się na kartce 🙂
Jeśli czegoś zapomnieliście, to kontaktujcie z nami przez dziennik elektroniczny lub mailowo.
23 marca 2020 r.
Temat: Pola czworokątów.
Zadania do wykonania:
19 marca 2020 r.
Temat: Czworokąty i ich własności.
Zadania do rozwiązania:
Materiały pomocnicze:
Rodzaje czworokątów i ich własności
16 marca 2020 r.
Temat: Trójkąty i ich własności.
Zadania do rozwiązania:
Materiały pomocnicze:
Lekcje wideo – wprowadzenie do trójkątów
Lekcje wideo – własności trójkątów, pole trójkąta
Zaglądajcie też na strony:
Khan Academy – platforma edukacyjna
Matzoo – Matematyczne Zoo – zadania i testy
Pi-stacja – Darmowe wideolekcje z matematyki