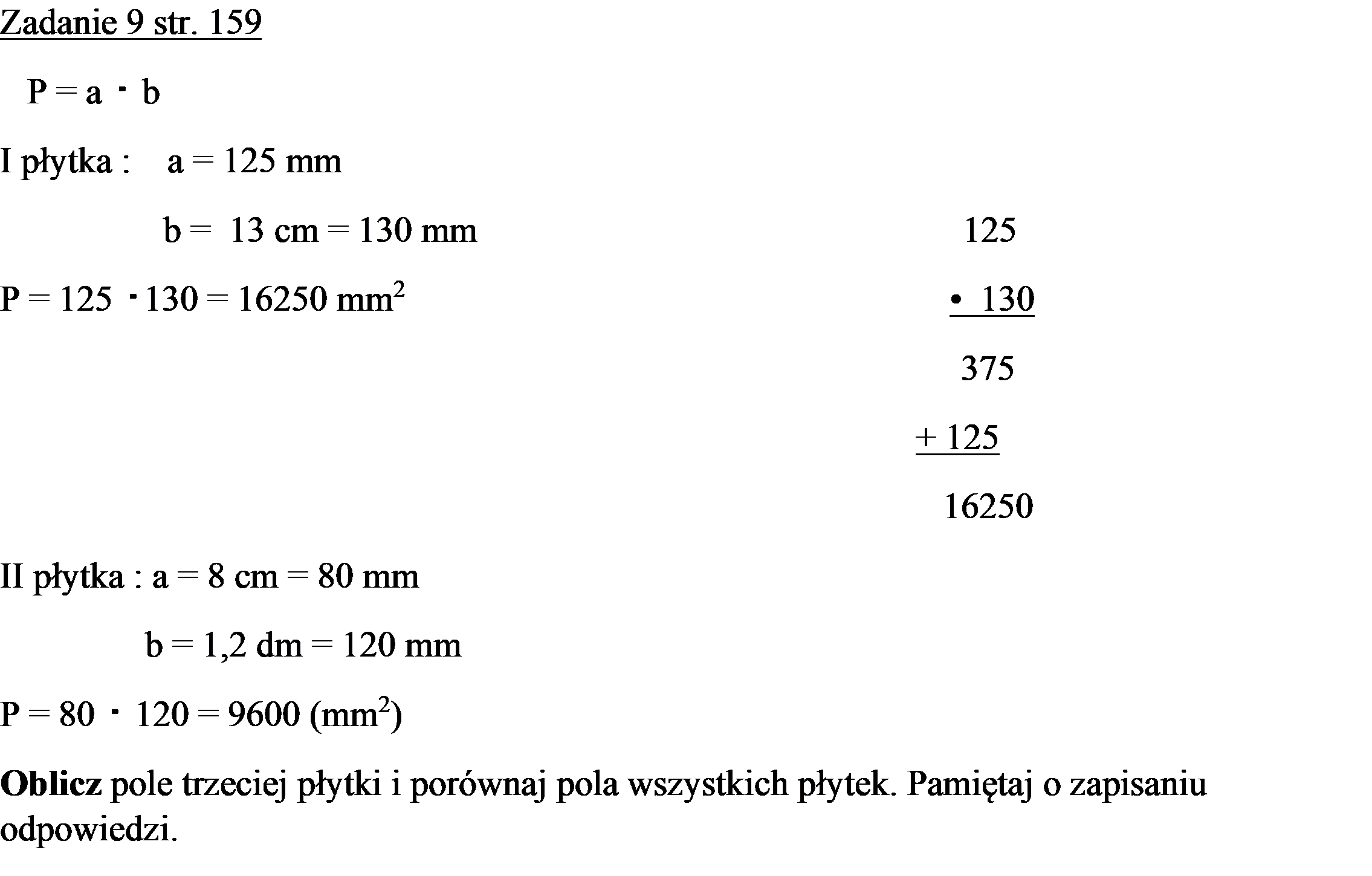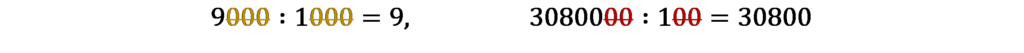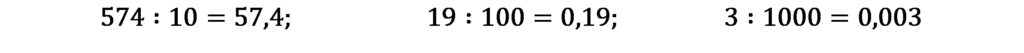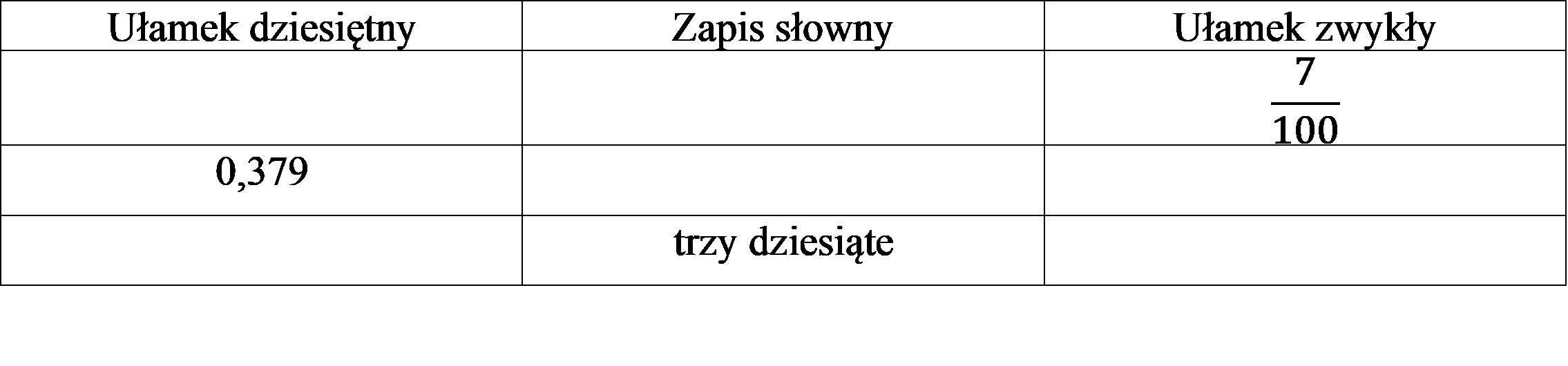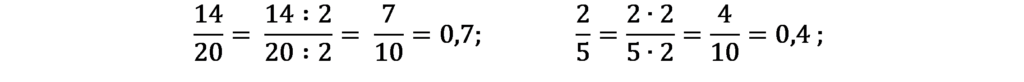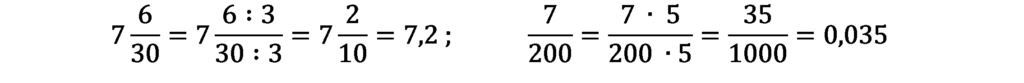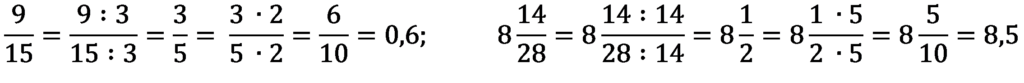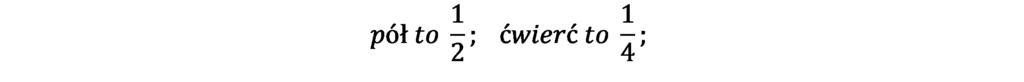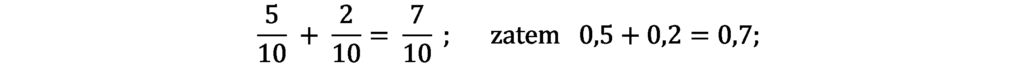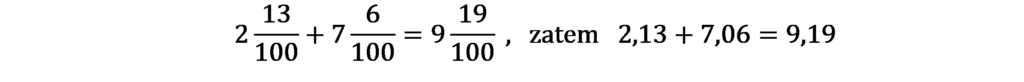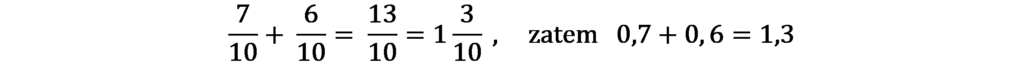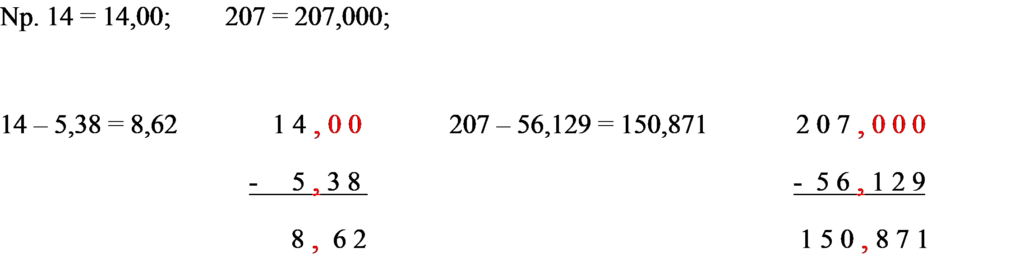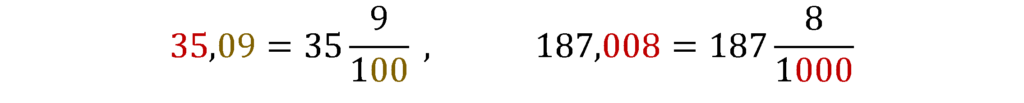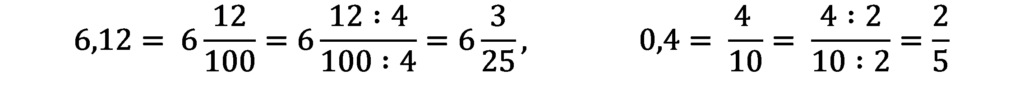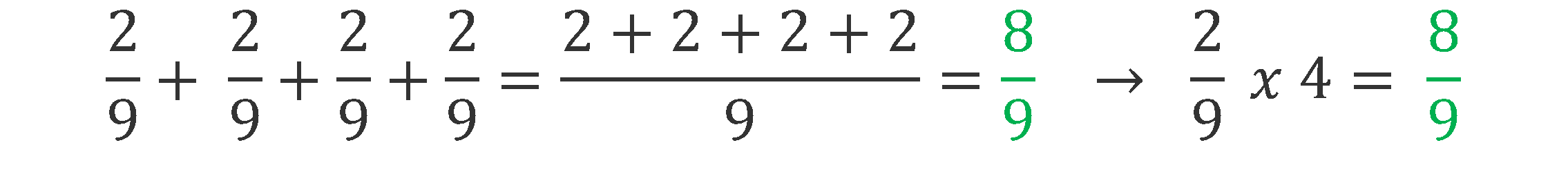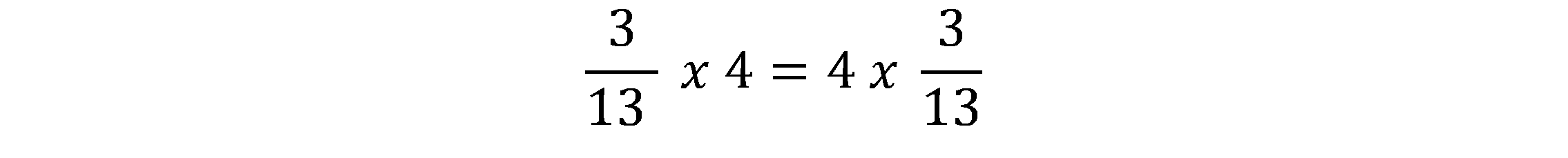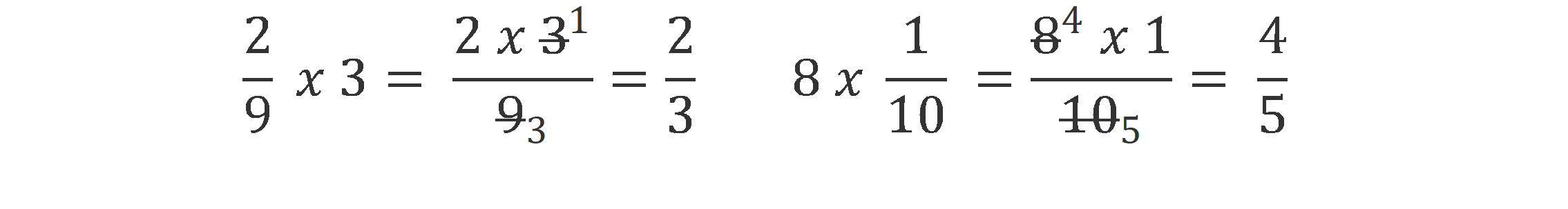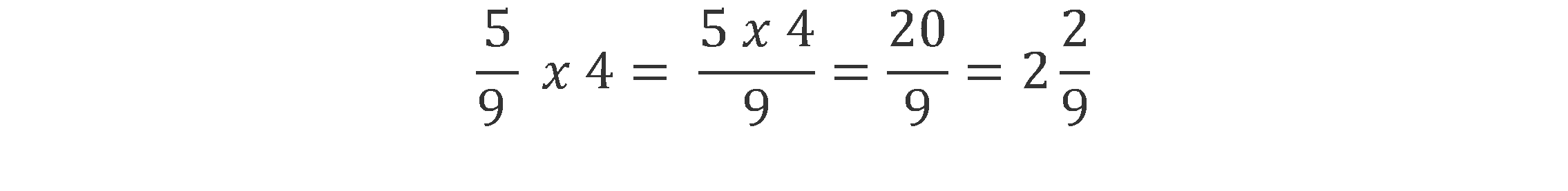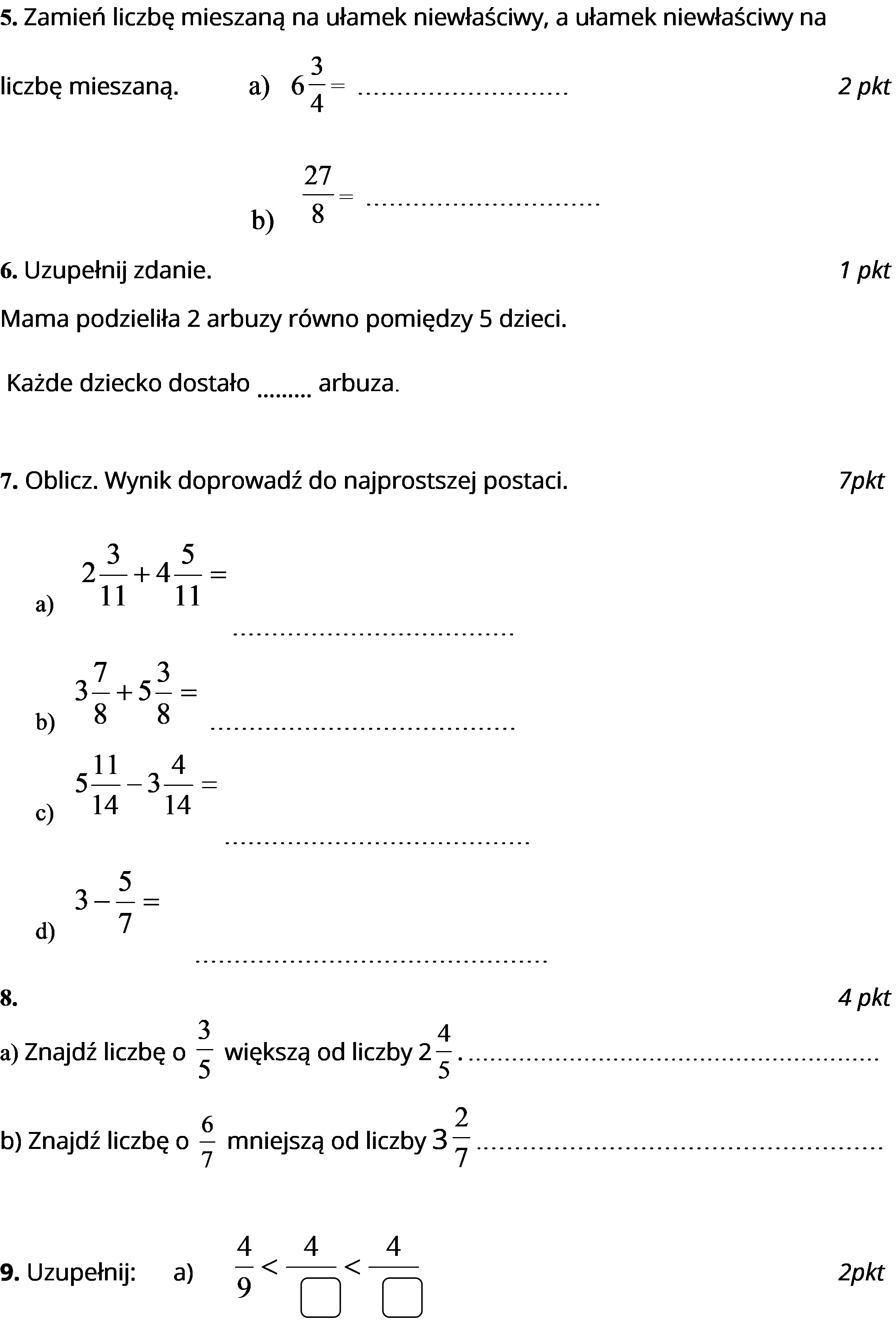Kochani Uczniowie klas czwartych!
zaczynamy nowy tryb pracy. Dla niektórych będzie to nowa lekcja, dla innych utrwalenie. Wkrótce jednak wszystko się wyrówna. Nie poddawajcie się i podejmijcie wyzwanie. Lekcje przepisujcie do zeszytu zgodnie z numeracją podaną niżej. Jeżeli będziecie mieć problemy z rozwiązaniem zadań jesteśmy do Waszej dyspozycji. Pytania możecie zadawać drogą e-mail, w Teamsie lub przez dziennik elektroniczny.
Mirosława Modzelewska miroslawa.modzelewska@sp2gk.onmicrosoft.com
Anna Nowak anna.nowak@sp2gk.onmicrosoft.com
WAŻNE! Do sprawdzenia będziecie przesyłać tylko wskazane przez nauczyciela zadania. Na odesłanie zadań macie 2 dni robocze od dnia, w którym odbywa się dana lekcja. Oznacza to, że jeżeli lekcja wypada w poniedziałek to pracę należy odesłać do środy, jeśli we wtorek to do czwartku, jeśli we środę to do piątku, jeśli w czwartek to do poniedziałku, jeśli w piątek to do wtorku.
Jeżeli nie możecie odesłać pracy w tym terminie, to koniecznie skontaktujcie się ze swoją nauczycielką.
Jeśli nie macie podręcznika w domu, to możecie skorzystać z dostępnego na stronie:
Tydzień obowiązywania: 22 – 25 czerwca
Lekcja 44
Temat: Różne bryły
Cel: Umiem nazywać różne bryły
Oprócz prostopadłościanów, o których już się uczyłeś, istnieje jeszcze wiele innych brył.
Naucz się rozpoznawać niektóre z nich.
Zapisz w zeszycie:
Graniastosłup – ma dwie takie same podstawy (dowolny wielokąt), a jego wszystkie ściany boczne są prostokątami.
Ostrosłup – ma jedną podstawę (dowolny wielokąt), a jego wszystkie ściany boczne są trójkątami o wspólnym wierzchołku.
Bryły obrotowe, np.: kula, stożek, walec – nie można w nich wskazać żadnych wielokątów.
Przyjrzyj się bryłom przedstawionym w zeszycie ćwiczeń na stronach 149 i 150 – wykonaj zapisane tam polecenia.
Warto obejrzeć filmik przedstawiający różne bryły:
https://www.youtube.com/watch?v=_S9MFPvK_-g
*Wersja do druku Lekcja 44 – Różne bryły
Lekcja 45
Temat: Objętość bryły
Cel: Wiem, co to jest objętość bryły.
Wiesz już jak wygląda sześcian.
Taki sześcian, którego krawędzie mają długości po: 1 mm albo po 1 cm, albo po 1 dm, albo po 1 m nazywamy sześcianami jednostkowymi.
Wykonaj w zeszycie rysunek:
Zapisz:
Jeśli krawędź sześcianu ma długość 10 cm czyli 1 dm to sześcian ma objętość 1 dm3 ( 1 decymetr sześcienny) – taką jednostkę nazywamy litrem
1 dm3 = 1 l (litr)
Objętość bryły równa jest liczbie jednostkowych sześcianików,
które ją całkowicie wypełniają.
Wykonaj ćwiczenia ze str. 152 i 153 w zeszycie ćwiczeń.
*Wersja do druku Lekcja 45 – Objętość bryły
Lekcja 46
Temat: Powtórzenie wiadomości o bryłach
Cel: Utrwalam zdobyte wiadomości o bryłach
Aby utrwalić zdobyte wiadomości o bryłach wykonaj ćwiczenia ze str. 155 i 156 w zeszycie ćwiczeń.
To już nasza ostatnia lekcja matematyki w tym roku szkolnym.
Bardzo różnił się przebieg tych 46 lekcji od poprzedniego, wszyscy musieliśmy się nauczyć pracować
w inny sposób.
Wymagało to do Was większej samodzielności, obowiązkowości, a także wsparcia Waszych Rodziców.
Mamy nadzieję, że staraliście się jak najwięcej skorzystać z Lekcji zdalnych umieszczanych na stronie internetowej szkoły. Będziecie mogli jeszcze do nich powracać (może warto mieć je wydrukowane?)
Nam też bardzo brakowało bezpośredniego kontaktu z Wami.
Dziękujemy Wam za Waszą współpracę.
Życzymy Wam udanych, radosnych wakacji i liczymy na spotkanie z Wami we wrześniu.
Do zobaczenia! 😊
Nauczycielki matematyki
*Wersja do druku Lekcja 46 – Powtórzenie wiadomości o bryłach
Tydzień obowiązywania: 15 – 19 czerwca
Lekcja 40 i 41
Temat: Obliczanie pól prostokątów -zadania tekstowe
Cel: – utrwalam umiejętność obliczania pola prostokąta
– ćwiczę umiejętność czytania ze zrozumieniem
– utrwalam reguły obowiązujące przy rozwiązywaniu zadań tekstowych:
- zapisywanie danych,
- zapisywanie wszystkich działań,
- zapisywanie wszystkich obliczeń (jeśli to konieczne także obliczeń pisemnych),
- zapisywanie odpowiedzi pełnym zdaniem
Przepisuj starannie wszystkie rozwiązania zapisane poniżej i wykonuj samodzielnie wskazane zadania. Rozłóż sobie tę pracę na dwa dni. Zadania są z podręcznika (jeśli Twoje podręczniki zostały już oddane, skorzystaj z linku do podręcznika umieszczonego na górze tej strony)
*Wersja do druku Lekcja 40 i 41 – Obliczanie pól prostokątów – zadania tekstowe
Lekcja 42 i 43
Temat: Prostopadłościan i sześcian
Cel: – umiem rozpoznawać prostopadłościany i sześciany
– umiem wskazać ścianę, wierzchołek i krawędź bryły
Najbliższe lekcje będą poświęcone bryłom, czyli figurom przestrzennym.
Najczęściej spotykane z nich to prostopadłościany, w ich kształcie są bardzo często opakowania, meble, budynki.
Obejrzyj rysunki na stronie 161 w podręczniku.
Rozejrzyj się wokół siebie i spróbuj znaleźć jak najwięcej przedmiotów w kształcie prostopadłościanu w twoim mieszkaniu i za oknem.
Obejrzyj filmik prezentujący omawiane dziś bryły:
https://pistacja.tv/film/mat00244-budowa-prostopadloscianu-i-szescianu?playlist=510
Przerysuj rysunki (licz kratki) wraz z opisem:
Wykonaj ćwiczenia ze str. 146, 147, 148 z zeszytu ćwiczeń
*Wersja do druku Lekcja 42 i 43 – Prostopadłościan i sześcian
Tydzień obowiązywania: 8 – 10 czerwca
Lekcja 38
Temat: Pole prostokąta
Cel: Znam metodę na obliczanie pola prostokąta, w tym kwadratu.
Wiecie już, że pole figury to liczba wypełniających ją jednostkowych kwadracików.
W przypadku figur o regularnych kształtach można uprościć sobie ich liczenie.
![]() Dla takiej figury łatwo jest po prostu kolejno liczyć ile jest kwadracików
Dla takiej figury łatwo jest po prostu kolejno liczyć ile jest kwadracików
– jest ich 8
Dla tej figury obliczenie staje się już żmudne i czasochłonne. 
Jeśli jednak zauważymy, że jest w niej 11 rzędów po 10 kwadracików,
to wystarczy, że pomnożymy 10 x 11 i otrzymamy liczbę wszystkich kwadracików – 110.
Czyli, aby obliczyć pole prostokąta wystarczy pomnożyć liczbę kwadracików na jednym boku przez liczbę kwadracików na drugim boku, zaś liczba tych kwadracików wyrażona jest długością danego boku.
Zatem:
Zrób rysunki i przepisz:
a
b P = a ⋅ b pole prostokąta o bokach długości a i b
a
Jeśli prostokąt jest kwadratem (czyli a = b) wzór przybiera postać:
a P = a ⋅ a pole kwadratu o boku a
P = a²
Wykonaj ćw. 1 ze str. 144 w zeszycie ćwiczeń
*Wersja do druku: Lekcja 38 – Pole prostokąta
Lekcja 39
Temat: Obliczanie pól prostokątów
Cel: umiem obliczać pola prostokątów
Znasz już sposób na obliczanie pola prostokąta – pora na przećwiczenie jego wykorzystania.
Przepisz wszystko, to co znajduje się poniżej:
Przy rozwiązywaniu zadań należy zawsze pamiętać o:
- wypisywaniu danych,
- zapisaniu stosowanych wzorów,
- zapisaniu podstawienia danych do wzoru,
- zapisaniu wszystkich obliczeń,
- zapisywaniu właściwych jednostek,
- zapisaniu odpowiedzi (pełnym zadaniem).
Zadanie 1 ze str.158
Poziom A
c) a = 4 cm
b = 2 cm
P = a ⋅ b, P = 4cm ∙ 2cm = 8 cm2
Odp. Pole tego prostokąta wynosi 8 cm2
Wykonaj teraz przykład a) z tego poziomu
Poziom B
c) a = 5 dm
b = 6 dm
P = a ∙ b, P = 5 ∙ 6 = 30 (dm2)
możesz nie zapisywać jednostek w działaniu, tylko w nawiasie w samym wyniku
Odp. Pole tego prostokąta wynosi 30 dm2
Wykonaj teraz przykład a) z tego poziomu
Poziom C
c) a = 15 dm
P = a2, P = 152 = 15 ∙ 15 = 225 (dm2)
Odp. Pole tego kwadratu wynosi 225 dm2
Wykonaj teraz przykład a) z tego poziomu
Poziom D
c) a = 40000 cm = 400 m
koniecznie należy zamienić jednostki, aby oba boki były wyrażone w takich samych
b = 6 m
P = a ∙ b, P = 400 ∙ 6 = 2400 (m2)
Odp. Pole tego prostokąta wynosi 2400 m2
Wykonaj teraz przykład a) z tego poziomu
Poziom Mistrz – tu należy obliczyć również obwód
c) a = 3 m = 30 dm
b = 4 dm
P = a ∙ b, P = 30 ∙ 4 = 120 (dm2)
Obw. = 2 ∙ (a + b) Obw.= 2 ∙ (30 + 4 ) = 2 ∙34 = 68 (dm)
Odp. Pole tego prostokąta wynosi 120 cm2,a jego obwód wynosi 68 cm
Wykonaj teraz przykład a) z tego poziomu (pamiętaj o zamianie jednostek)
*Wersja do druku: Lekcja 39 – Obliczanie pól prostokątów
Tydzień obowiązywania: 1- 5 czerwca
Lekcja 34
Temat: Pole figury
Cel.: Rozumiem pojęcie „pole figury”
Dziś poznajesz nowe określenie – pole figury – to bardzo ważne, aby je dobrze zrozumieć, bo będzie pojawiało się bardzo często; na lekcjach matematyki i nie tylko.
Przyjrzyj się dokładnie rys. na str. 146 w podręczniku i zastanów się, która z tych ozdób jest największa,
a która najmniejsza – nie jest to wcale takie proste…
Chyba, że podzielimy je sobie na jednakowe kwadraciki, jak na rysunku:
Teraz wystarczy tylko policzyć, z ilu kwadracików składa się każda
z figur i będziemy mogli porównać ich wielkości.
Zapisz w zeszycie odpowiedź na wcześniejsze pytanie.
Przepisz do zeszytu (w wyróżniający się sposób) poniższe zdanie:
Pole figury określa jej wielkość, czyli to, ile miejsca zajmuje ona płaszczyźnie.
Wykonaj zadania z podręcznika: 1 ze str. 148, 2, 3, 4 i 5 ze str. 149 (odpowiadaj pełnymi zdaniami)
Pamiętaj, że figury o takim samym polu, mogą mieć bardzo różne kształty.
*Wersja do druku: Lekcja 34 – Pole figury
Lekcja 35
Temat: Pole figury – ćwiczenia
Cel.: Umiem określać pole figury dzieląc ją na kwadraty jednostkowe
Na tej lekcji utrwalasz znajomość pojęcia pole figury wykonując związane z nim ćwiczenia
Wykonaj w zeszycie ćwiczeń : ćw. ze str. 137, 138, 139.
*Wersja do druku: Lekcja 35 – Pole figury – ćwiczenia
Lekcja 36
Temat: Jednostki pola
Cel.: Wiem w jakich jednostkach może mierzyć pole figury
Wiesz już, że aby porównać pola różnych figur możemy podzielić je na jednakowe kwadraciki
i porównać ich liczby.
Przepisz do zeszytu (w wyróżniający się sposób) poniższe zdanie:
Pole figury to liczba kwadracików jednostkowych, które ją całkowicie wypełniają.
Mogłoby się zdarzyć, że różne osoby podzieliły tę samą figurę na innej wielkości kwadraciki i takie same figury miałyby pola wyrażone innymi liczbami kwadracików- porównanie ich byłoby więc błędne, aby uniknąć takich problemów ustalono wielkości stosowanych kwadracików, są to:
Przepisuj wszystko do zeszytu:
Kwadrat o boku 1cm  jest to centymetr kwadratowy
jest to centymetr kwadratowy
(narysuj go) zapisujemy to tak: 1cm2
Jeśli kwadrat będzie miał boki o długości 1 dm,
to będzie to decymetr kwadratowy czyli 1dm2
Jeśli kwadrat będzie miał boki o długości 1 m,
to będzie to metr kwadratowy czyli 1m2
Jeśli kwadrat będzie miał boki o długości 1 km,
to będzie to kilometr kwadratowy czyli 1km2
Jeśli kwadrat będzie miał boki o długości 1 mm,
to będzie to milimetr kwadratowy czyli 1mm2
Dobór jednostki zależy od wielkości figury, której pole chcemy podać (wybieramy najwygodniejszą):
Zapisz pełnymi zdaniami odpowiedzi na pytania z zad. 2 ze str. 152 w podręczniku
Wykonaj zad. 4 i 5 ze str. 153
*Wersja do druku: Lekcja 36 – jednostki pola
Lekcja 37
Temat: Jednostki pola – ćwiczenia
Cel.: Utrwalam znajomość jednostek pola
Aby utrwalić umiejętność odczytywania pola figury z rysunku i rysowania figur o danym polu na papierze w kratkę wykonaj:
z podręcznika: zad. 7 ze str. 153, 9 ze str. 154
w zeszycie ćwiczeń: ćw. ze str. 140 i 141 (dla chętnych także ze 142)
*Wersja do druku: Lekcja 37- Jednostki pola – ćwiczenia
Tydzień obowiązywania: 25- 29 maja
Lekcja 30
Temat: Mnożenie i dzielenie przez 10, 100, 1000…
Cel: Umiem w prosty sposób pomnożyć i podzielić ułamek dziesiętny przez liczby typu:
10. 100, 1000…
Umiecie już mnożyć i dzielić liczby naturalne przez liczby typu 10, 100, 1000….
Gdy mnożymy – dopisujemy na końcu tyle zer, ile ich jest za 1
Gdy dzielimy – skreślamy na końcu tyle zer, ile ich jest za 1
Np.: (zapisz w zeszycie wszystko to, co znajduje się poniżej, stosując wyróżnienia)
dopisujemy po dwa zera dopisujemy po sześć zer
skreślamy po trzy zera skreślamy po dwa zera
Gdy chcemy pomnożyć ułamek dziesiętny przez 10, 100, 1000… przesuwamy przecinek w prawo o tyle miejsc, ile jest zer za 1.
jedno zero – przecinek przesuwa się trzy zera – przecinek przesuwa się
o jedno miejsce o trzy miejsca
w razie potrzeby należy dopisać na końcu odpowiednią liczbę zer, np.:
Gdy chcemy podzielić ułamek dziesiętny przez 10, 100, 1000… przesuwamy przecinek w lewo o tyle miejsc, ile jest zer za 1.
Np.:
jedno zero – przecinek przesuwa się dwa zera – przecinek przesuwa się
o jedno miejsce o dwa miejsca
w razie potrzeby należy z przodu dopisać odpowiednią liczbę zer, np.:
liczba naturalna ma przecinek na końcu, a więc, np.:
W zrozumieniu i utrwaleniu poznanych zasad mogą pomóc Ci filmiki:
https://www.youtube.com/watch?v=7_gFDt9VOeg
https://www.youtube.com/watch?v=3ERW0tfP1LU
Wykonaj po dwa przykłady z każdego poziomu zad. 1 ze str. 137 w podręczniku (porównuj swoje wyniki z odpowiedziami) oraz zad. 2 i 7 ze str. 138 (pamiętaj o zapisywaniu wszystkich działań, a w zad. 7 również słownej odpowiedzi
* Wersja do druku: Lekcja 30d – mnożenie i dzielenie przez 10, 100 …
Lekcja 31
Temat: Utrwalanie wiadomości o ułamkach dziesiętnych
Cel: – swobodnie posługuję się ułamkami dziesiętnymi (ich zapisem, odczytywaniem
i porównywaniem),
– doskonalę umiejętność rozwiązywania zadań tekstowych – czytania ze zrozumieniem,
analizowania treści zadania, zapisywania wszelkich obliczeń i odpowiedzi
Wykonaj w zeszycie zadania z podręcznika: 5 i 6 ze str. 115; 2, 3 i 5 ze str.119
Czytaj dokładnie polecenia, zapisuj całe przykłady, odpowiedzi zapisuj pełnymi zdaniami.
*Wersja do druku:Lekcja 31d – Utrwalanie wiadomości o ułamkach dziesiętnych
Lekcja 32
Temat: Doskonalenie umiejętności wykonywania działań na ułamkach dziesiętnych
Cel: – umiem sprawnie dodawać i odejmować ułamki dziesiętne oraz mnożyć je i dzielić
przez liczby typu 10, 100, 1000…
– doskonalę umiejętność rozwiązywania zadań tekstowych – czytania ze zrozumieniem,
analizowania treści zadania, zapisywania wszelkich obliczeń i odpowiedzi
Wykonaj w zeszycie zadania z podręcznika: zad. 8 i 9 ze str. 129; zad. 8 ze str. 140
zad. 15 ze str. 141
Jeśli chcesz spróbuj też czegoś trudniejszego: zad. 10/129 (pamiętaj o zamianie jednostek)
zad. 8 ze str. 138, zad. 5 ze str. 144
Czytaj dokładnie polecenia, zapisuj całe przykłady, odpowiedzi zapisuj pełnymi zdaniami.
*Wersja do druku: Lekcja 32d – Doskonalenie umiejetności wykonywania działań na ułamkach dziesiętnych
Lekcja 33
Temat: Czy już umiem? Sprawdzian – ułamki dziesiętne
Cel: – oceniam poziom swoich umiejętności związanych z ułamkami dziesiętnymi
– dowiaduję się od nauczycielki oceniającej moją pracę, co jeszcze muszę uzupełnić
Czas na wykazanie się nabytą wiedzą i umiejętnościami.
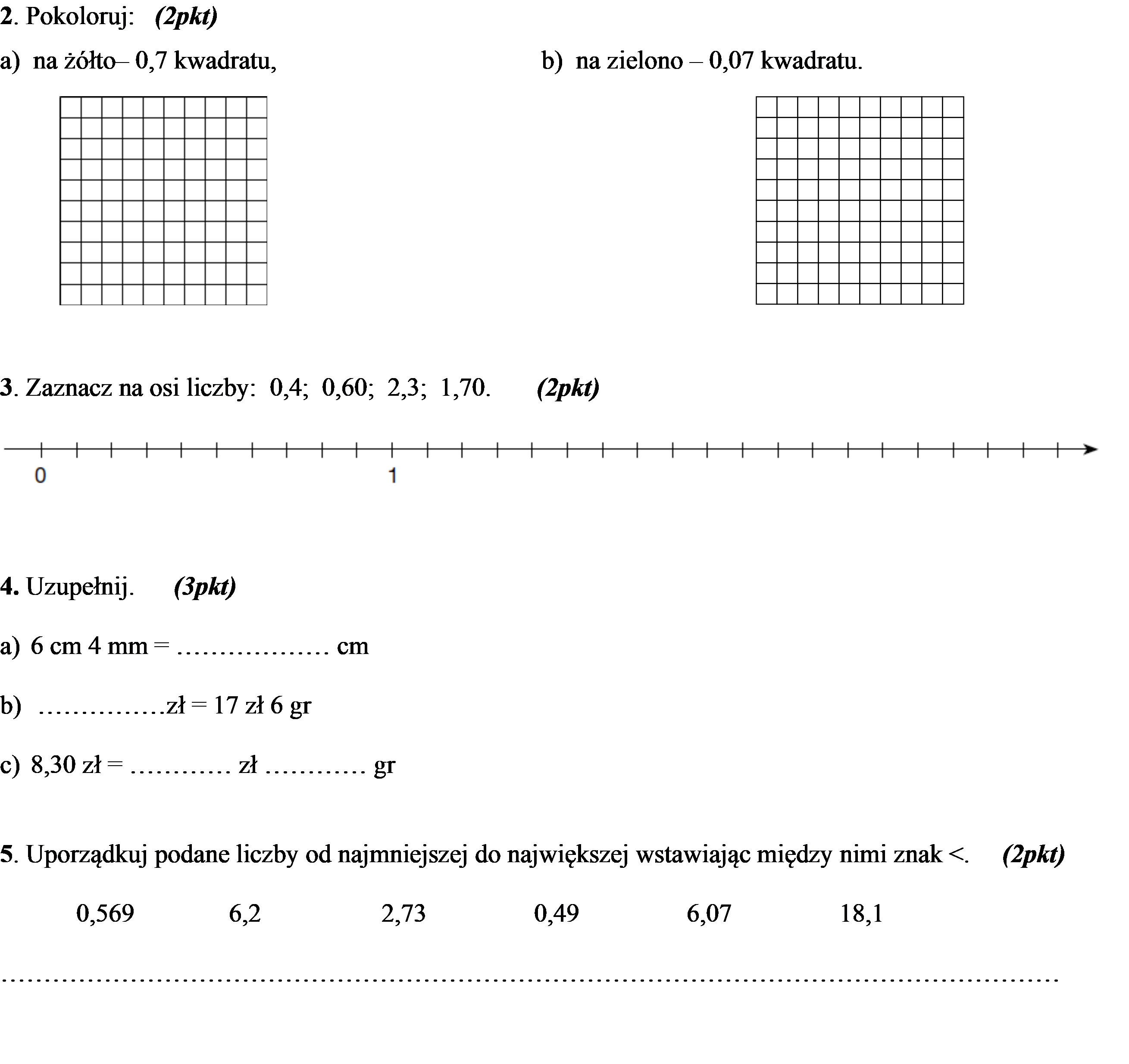
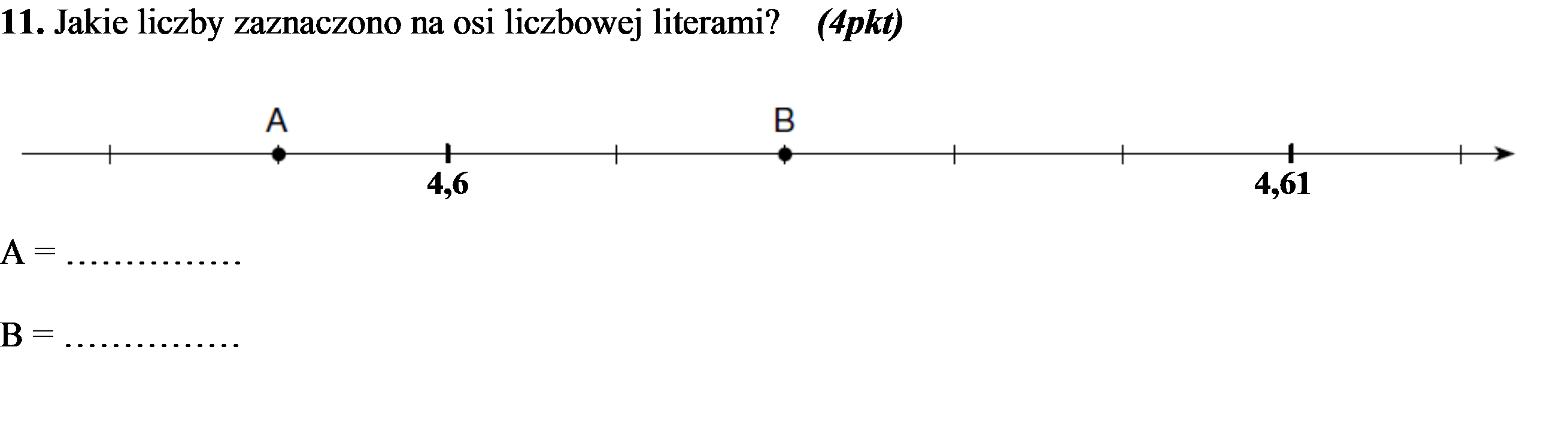
SPRAWDZIAN 6 – Ułamki dziesiętne 41 pkt
1. Uzupełnij tabelę. (3pkt)
Pracę prześlij swojej nauczycielce matematyki najpóźniej w przeciągu 2 dni roboczych od dnia, kiedy odbywa się ta lekcja za pomocą Teams lub na maila.
Link do sprawdzianu – otwórz , możesz także wydrukować:
Sprawdzian – pdf spr. kl. 4 ułamki dziesiętne d
Pamiętaj o dokładnym czytaniu poleceń, zapisywaniu wszystkich wykonywanych działań (nie tylko samych wyników!), w zadaniach tekstowych – odpowiedzi pełnym zadaniem.
Powodzenia 😊
*Wersja do druku:Lekcja 33d Czy już umiem…
Tydzień obowiązywania: 18- 22 maja
Lekcja 26
Temat: Zamiana ułamków
Cel: Umiem zamienić niektóre ułamki zwykłe na ułamki dziesiętne
Niektóre ułamki zwykłe potrafisz już zapisać jako ułamki dziesiętne, np.:
Poniższe przykłady przepisz uzupełniając samodzielnie:
Te przykłady nie sprawiły Ci raczej dużej trudności. Pora teraz na coś trudniejszego:
Jeśli ułamek zwykły nie ma w mianowniku liczby typu 10, 100, 1000, itp., należy go najpierw przekształcić (skrócić lub rozszerzyć), tak aby zyskał tego typu mianownik, np.:
Przepisz poniższe przykłady:
Czasami trzeba wykonać więcej kroków, np.:
Warto zapamiętać zamianę niektórych często używanych ułamków i stosować ją bez wykonywania obliczeń.
Zapoznaj się z Dobrą radą na str. 122 podręcznika i przepisz (w wyróżniający się sposób) przykłady zapisane przy pierwszej kropce.
Niektórych ułamków zwykłych nie da się zamienić na ułamki dziesiętne przy pomocy skracania lub rozszerzania – co można wtedy zrobić dowiesz się w klasach starszych.
Wykonaj po trzy przykłady z poziomu A i B zad. 2 ze str. 123 w podręczniku, zad. 3 ze str. 123 i zad. 6 ze str. 124 – pamiętaj o sprawdzaniu wyników z odpowiedziami
*Wersja do druku: Lekcja 26d – zamiana ułamków
Lekcja 27
Temat: Dodawanie ułamków dziesiętnych
Cel: Umiem dodawać ułamki dziesiętne w pamięci i pisemnie
Przyjrzyj się dokładnie ilustracji na str. 125 podręcznika, odpowiedz na pytania zapisane na białym tle (nie zapisuj nic w zeszycie).
Umiesz już dodawać ułamki zwykłe o takich samych mianownikach – dodajemy liczniki,
a mianownik pozostawiamy bez zmian.
Przeanalizuj i przepisz do zeszytu wszystkie przykłady:
Wiesz już, że na końcu ułamka dziesiętnego możemy dopisywać dowolną liczbę zer, jeśli więc dodawane liczby mają różną liczbę cyfr po przecinku możesz uzupełnić braki zerami.
2,3 + 4,14 = 2,30 + 4,14 = 6,44; 21,754 + 0,1 = 21,754 + 0,100 = 21,854
Trudniejsze dodawanie możesz wykonywać pisemnie – zapamiętaj (i przepisz do zeszytu) bardzo ważną zasadę:
Dodając pisemnie ułamki dziesiętne podpisujemy je tak, aby przecinek znalazł się
pod przecinkiem.
Wykonaj po dwa przykłady z poziomów A, B, C, D z zad. 1 i przykłady a, c, f, i z zad. 2 ze str. 128 w podręczniku – pamiętaj o sprawdzaniu wyników z odpowiedziami
*Wersja do druku: Lekcja 27 – dodawanie ułamków dziesiętnych
Lekcja 28
Temat: Odejmowanie ułamków dziesiętnych
Cel: Umiem odejmować ułamki dziesiętne w pamięci i pisemnie
Zasady obowiązujące podczas odejmowania ułamków dziesiętnych są takie same, jak przy ich dodawaniu (zajrzyj do notatek z lekcji 28.)
Aby przypomnieć sobie odejmowanie pisemne przeanalizuj dokładnie przykłady ze str. 132 w podręczniku.
Pamiętaj o tym, że każdą liczbę całkowitą możemy zapisać w postaci dziesiętnej zaznaczając na jej końcu przecinek i dopisując dowolną liczbę zer (zapisz w zeszycie poniższe przykłady).
Wykonaj po dwa przykłady z każdego poziomu zad. 1 ze str. 133
i przykłady a, d, g, h z zad. 1 ze str. 133 – pamiętaj o sprawdzaniu wyników z odpowiedziami
*Wersja do druku: Lekcja 28d – odejmowanie ułamków dziesiętnych
Lekcja 29
Temat: Dodawanie i odejmowanie ułamków dziesiętnych – zadania tekstowe
Cel: Umiem dodawać i odejmować ułamki dziesiętne w sytuacjach praktycznych
Na tej lekcji utrwalaj umiejętność czytania ze zrozumieniem i analizowania tekstu zadania oraz dodawania i odejmowania ułamków dziesiętnych.
Wykonaj w zeszycie zadania z podręcznika: 8 i 9 ze str. 129 oraz 4 ze str. 133 i 5 ze str. 134
Pamiętaj o pisaniu odpowiedzi (pełnymi zdaniami)!
*Wersja do druku: Lekcja 29d – dodawanie i odejmowanie ułamków dziesiętnych
Tydzień obowiązywania: 11- 15 maja
Lekcja 22
Temat: Ułamek dziesiętny
Cel: – umiem odczytywać ułamki dziesiętne
– umiem zapisywać ułamki dziesiętne
Od tej lekcji rozpoczynacie zdobywanie wiedzy na temat ułamków dziesiętnych i nabywanie umiejętności wykonywania działań na nich i praktycznego posługiwania się nimi.
Z tymi ułamkami spotykaliście się już w życiu codziennym – najczęściej przy zakupach, bo korzysta się z nich np. przy zapisywaniu cen towarów.
Ułamek dziesiętny zamiast kreski ułamkowej posiada przecinek, a jego mianownik jest niewidoczny, ale łatwy do odkrycia – jest to zawsze 1 z zerami (z prawej strony), tych zer jest tyle, ile cyfr znajduje się po przecinku (z prawej strony). Liczba przed przecinkiem (z jego lewej strony) oznacza całości.
Np.: (zapisz te przykłady w zeszycie)
2 cyfry 2 zera 1 cyfra 1 zero
2 cyfry 2 zera 3 cyfry 3 zera
Zapamiętaj: (zapisz w zeszycie w wyróżniający się sposób):
Jedna cyfra po przecinku oznacza części dziesiąte, np.:
2,4 – dwie całe i cztery dziesiąte, 10,8 – dziesięć całych i osiem dziesiątych
Dwie cyfry po przecinku oznaczają części setne, np.:
2,04 dwie całe i cztery setne, 5,12 – pięć całych i dwanaście setnych
Trzy cyfry po przecinku oznaczają części tysięczne, np.;
2,004 dwie całe i cztery tysięczne; 9,047 – dziewięć całych i czterdzieści siedem tysięcznych
Zauważ, że w zapisie ułamka zwykłego nigdy nie pisze się 0 całych, przy zapisie ułamka dziesiętnego to 0 musi być napisane (musi być coś przed przecinkiem); nie musimy go jednak czytać,
- 0,05 możemy odczytać: zero całych i pięć setnych lub po prostu: pięć setnych
Aby utrwalić poznane zasady wykonaj: przykłady z poziomu A zad. 1 ze str. 114,
i zad. 4 ze str. 115.
*Wersja do druku Lekcja 22d – ułamek dziesiętny
Lekcja 23
Temat: Ćwiczenia związane z zapisem ułamka dziesiętnego
Cel: utrwalam umiejętność zapisywania i odczytywania ułamków dziesiętnych
Zapoznaj się z Dobrą radą ze str. 114: przeanalizuj dokładnie, to co zapisano w zielonej ramce i pod nią.
Wykonaj po trzy przykłady z poziomów B, C i D z zad. 1 ze str. 114.
Jeśli chcesz spróbować czegoś trudniejszego, zrób też kilka przykładów z poziomu Mistrz (warto tu zamienić najpierw ułamki niewłaściwe na liczby mieszane).
Wykonaj zad. 3 ze str. 115 (zastanów się najpierw jaką częścią całego kwadratu jest jeden pasek, a jaką jeden kwadracik)
*Wersja do druku: Lekcja 23d -ułamek dziesiętny – ćwiczenia
Lekcja 24
Temat: Porównywanie ułamków dziesiętnych
Cel: umiem porównywać ułamki dziesiętne
Przyjrzyj się dwóm kwadratom narysowanym na stronie 117, przeanalizuj to, co napisano pod nimi, a następnie przepisz do zeszytu pogrubiony tekst.
Przeanalizuj wyjaśnienia zapisane w górnej połowie strony 118
Warto też obejrzeć filmik:
Aby sprawdzić, czy dobrze zrozumiałeś przedstawione zasady porównywania ułamków dziesiętnych
wykonaj: po trzy pkt z poziomów A, B i C z zad. 1 ze str. 118 (porównuj swoje wyniki z odpowiedziami) i zad. 4 ze str. 119.
*Wersja do druku: Lekcja 24d – porównywanie ułamków dziesiętnych
Lekcja 25
Temat: Zamiana ułamków
Cel: umiem zamienić ułamek dziesiętny na nieskracalny ułamek zwykły
Umiesz już wyrażać ułamki na dwa sposoby zwykły i dziesiętny – czyli zastępować ułamek kreską ułamkową i odwrotnie.
Przy zamianie ułamków dziesiętnych na zwykłe należy jeszcze sprawdzić, czy otrzymanego ułamka zwykłego nie można skrócić, np.:
Zapisz te przykłady w zeszycie:
Warto obejrzeć filmik:
https://www.youtube.com/watch?v=CYpBLkq0s7A
Wykonaj po trzy przykłady z każdego poziomu z zad. 1 ze str. 123.
*Wersja do druku: Lekcja 25d -zamiana ułamków dziesietnych na zwykłe
Tydzień obowiązywania: 4 – 8 maja
Lekcja 18
Temat: Mnożenie ułamków przez liczby naturalne
Cel: Umiem pomnożyć ułamek przez liczbę naturalną
Umiecie już dodawać ułamki o takich samych mianownikach, a pamiętacie zapewne, że dodawanie takich samych składników można zastąpić mnożeniem (przepisuj wszystkie przykłady):
7 + 7 + 7 + 7 + 7 + 7 + 7+ 7+ 7 = 7 x 9
podobnie:
Przepisz do zeszytu (w wyróżniający się sposób) tekst:
Aby pomnożyć ułamek przez liczbę naturalną należy
pomnożyć przez nią jego licznik, a mianownik przepisać bez zmian.
Pamiętaj też, że:
Mnożenie jest przemienne, zatem:
Czasami mnożenie można uprościć (warto to robić zawsze, gdy to jest możliwe
– czyli gdy w liczniku i mianowniku znajdują się liczby mające wspólny dzielnik)
Jeśli iloczyn będzie ułamkiem niewłaściwym należy zamienić go na liczbę mieszaną lu naturalną
Dla przećwiczenia wykonaj po dwa przykłady z zad. 1 ze str. 101 i 102 – z każdego poziomu; nie zapomnij o sprawdzeniu swoich wyników z tymi w odpowiedziach na końcu podręcznika.
*Wersja do druku Lekcja 18 – Mnożenie ułamków zwykłych przez liczby naturalne
Lekcja 19 i 20
Temat: Utrwalanie wiadomości i umiejętności związanych z ułamkami zwykłymi.
Cel: Doskonalenie znajomości ułamków zwykłych i umiejętności wykonywania na nich działań.
Zadania do wykonania:
Podczas tej lekcji ćwiczcie wykonując zadania ze str. 104 i 105 z podręcznika (z zad. 1, 2, 3, 4, 5, 6, 9, 10, 11, 12, 15 – przynajmniej po dwa podpunkty, z pozostałych zadań- całość); jeśli je zrobisz i chcesz jeszcze udoskonalić swoje umiejętności możesz wykonać zadania ze str. 105.
*Wersja do druku Lekcja 19 i 20 – Utrwalanie wiadomości i umiejętności związanych z ułamkami zwykłymi
Lekcja 21
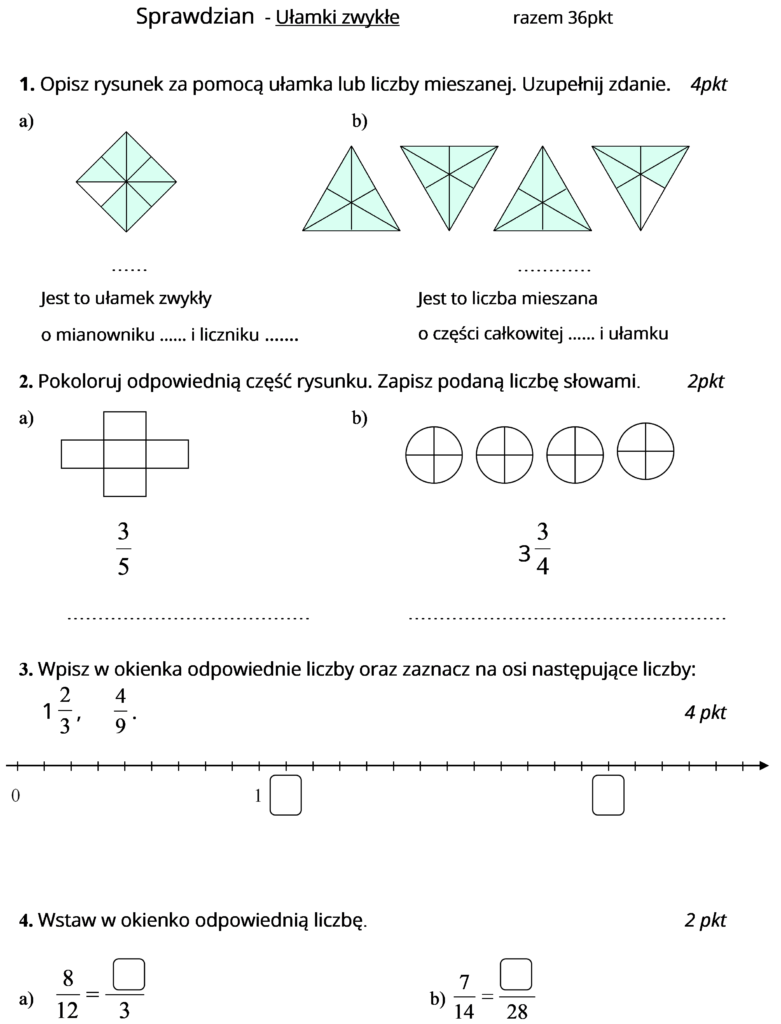
Temat: Sprawdzian – Ułamki zwykłe
Cel: Wiem w jakim stopniu opanowała/em wiadomości i umiejętności związane
z ułamkami zwykłymi i co jeszcze muszę uzupełnić.
Wykonaj poniższe zadania (czytaj dokładnie polecenia).
Rozwiązania prześlij swojej nauczycielce matematyki najpóźniej w przeciągu 2 dni roboczych
od dnia, kiedy odbywa się ta lekcja.
*Wersja do druku Lekcja 21 – Sprawdzian, ułamki zwykłe
Tydzień obowiązywania: 27 – 30 kwietnia
Lekcja 15
Temat: Dodawanie ułamków o takich samych mianownikach
Cel: Umiem dodawać ułamki o takich samych mianownikach
Zadania do wykonania:
Przeanalizuj przykłady przedstawione na rysunkach na stronie 94.
Przepisz do zeszytu (w wyróżniający się sposób) tekst z niebieskiej ramki umieszczony nad rysunkami, a następnie poniższe przykłady:
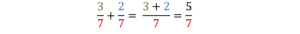
Zwróć uwagę, że czasami w obliczonej sumie można jeszcze wyciągnąć całości lub skrócić ułamek:
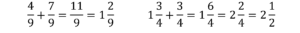
W zapamiętaniu tej zasady może być pomocny filmik:
https://www.youtube.com/watch?v=GvVgKE3y2Aw
W celu przećwiczenia wykonaj: przykłady a, b, c z poziomów A, B, C z zadania 1 ze str. 96.
Pamiętaj o sprawdzeniu wyników z odpowiedziami na końcu książki.
A może spróbujesz jeszcze wykonać po dwa przykłady z poziomów D i MISTRZ?
*Wersja do wydruku Lekcja 15 – Dodawanie ułamków o takich samych miamownikach
Lekcja 16
Temat: Odejmowanie ułamków o takich samych mianownikach
Cel: Umiem odejmować ułamki o takich samych mianownikach
Zadania do wykonania:
Przeanalizuj przykłady umieszczone na stronie 95 podręcznika.
Przepisz do zeszytu (w wyróżniający się sposób) tekst z niebieskiej ramki umieszczony nad rysunkami, a następnie poniższe przykłady:
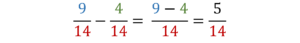
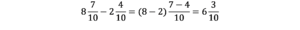
Czasami należy wykonać jeszcze dodatkowe czynności – gdy licznik pierwszego ułamka (odjemnej) jest mniejszy od licznika drugiego ułamka (odjemnika):
Możemy wtedy jedną całość z odjemnej zamienić na ułamek, np. (zapisz ten przykład w zeszycie)
![]()
Wykonaj przykłady a i b z zadania 8 ze str. 98 podręcznika
Dla utrwalenia obejrzyj filmik:
https://www.youtube.com/watch?v=gvyok5WvuxE
https://www.youtube.com/watch?v=LKeNwmL-FEE
Dla przećwiczenia wykonaj przykłady a, b, c z poziomów A, B, C z zad. 2 ze str. 96 i 97 podręcznika.
A może spróbujesz jeszcze wykonać po dwa przykłady z poziomów D, E i MISTRZ?
*Wersja do wydruku Lekcja 16 – Odejmowanie ułamków o takich samych mianownikach (1)
Lekcja 17
Temat: Dodawanie i odejmowanie ułamków o takich samych mianownikach –
zadania tekstowe
Cel: utrwalam umiejętności związane z ułamkami zwykłymi.
Zadania do wykonania:
Dla powtórzenia ostatnio zdobytych wiadomości obejrzyj prezentację: po pobraniu i uruchomieniu pokazu slajdów klikaj na slajdzie – zmiany nie pojawiają się automatycznie, abyś mógł czytać i analizować we własnym tempie
Wykonaj zadania z podręcznika: 5 ze str. 97, 12 ze str. 99
*Wersja do wydruku Lekcja 17 – Dodawanie i odejmowanie ułamków – zadania tekstowe
Tydzień obowiązywania: 20 – 24 kwietnia 2020 r.
Lekcja 11
Temat: Liczby mieszane
Cel:
– znam i rozróżniam pojęcia: ułamek właściwy i ułamek niewłaściwy,
– wiem kiedy ułamek można zapisać w postaci liczby mieszanej,
Mówiąc „ułamek” myślimy zazwyczaj o czymś, co jest tylko fragmentem jakiejś całości – takie ułamki nazywamy właściwymi, ale mogą być też takie ułamki, które są większe od całości -takie ułamki nazywamy niewłaściwymi.
Przeanalizuj dokładnie wyjaśnienia znajdujące się na stronie 84 podręcznika.
Zapisz w zeszycie:
Ułamki właściwe to takie ułamki, w których licznik jest mniejszy od mianownika, np. 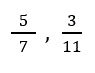 Dopisz jeszcze trzy własne przykłady ułamków właściwych.
Dopisz jeszcze trzy własne przykłady ułamków właściwych.
Ułamki niewłaściwe to takie ułamki, w których licznik jest większy od mianownika lub jemu równy np.
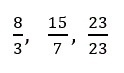
Dopisz jeszcze trzy własne przykłady ułamków niewłaściwych.
Liczby mieszane zawierają część całkowitą i część ułamkową, np.
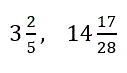
Dopisz jeszcze trzy własne przykłady liczb mieszanych.
W jeszcze lepszym zrozumieniu i utrwaleniu umiejętności zdobywanych na dzisiejszej lekcji może dopomóc Ci filmik: https://www.youtube.com/watch?v=D_jXNwkXcGg
*Wersja do wydruku Lekcja 11 – Liczby mieszane
Lekcja 12
Temat: Zamiana ułamków niewłaściwych na liczby mieszane i liczb mieszanych na ułamki niewłaściwe.
Cel: – umiem zamieniać ułamki niewłaściwe na liczby mieszane
– umiem zamieniać liczby mieszane na ułamki niewłaściwe
Aby zrozumieć jak można zamienić ułamek niewłaściwy na liczbę mieszaną przeanalizuj przykłady podane na str. 85 i poziom C ze str. 86
Gdy chcesz zamienić ułamek niewłaściwy na liczbę mieszaną musisz zastanowić się ile razy mianownik zmieści w liczniku i jaka pozostanie reszta, np.: (zapisz w zeszycie poniższy przykład wraz z wyjaśnieniem i kolorami)

W utrwaleniu umiejętności może pomóc Ci filmik:
Aby sprawdzić czy dobrze zrozumiałeś powyższe czynności wykonaj po cztery przykłady z zad. 1 ze str. 87 z poziomu B i C.
*Wersja do wydruku Lekcja 12 – Zamiana liczb mieszanych na ułamki niewłaściwe i odwrotnie
Lekcja 13
Temat: Ułamek jako iloraz
Cel: – umiem przedstawić ułamek jako iloraz liczb naturalnych, a iloraz liczb naturalnych jako ułamek
Warto przypomnieć, że iloraz to wynik dzielenie, ale również nazwa tego działania.
Na początek przeczytaj uważnie tekst na str. 89 podręcznika i postaraj się wykonać umieszczone tam polecenia.
Zapisz w zeszycie:
Kreska ułamkowa zastępuje znak dzielenia. Na przykład:
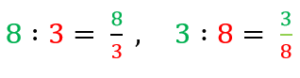
Dopisz jeszcze trzy własne przykłady.
Następnie przyjrzyj się dokładnie rysunkom i ich opisom na str. 90.
Dla lepszego zrozumienia warto obejrzeć filmik:
Aby poćwiczyć wykonaj po trzy przykłady z zad. 1 ze str. 91 (poziom A i B) i zad. 2 ze str. 92.
Jeśli dobrze sobie poradziłeś spróbuj jeszcze wykonać po trzy przykłady z poziomów C i D z zad 1 (str. 91 i 92)
*Wersja do wydruku Lekcja 13 – Ułamek jako iloraz
Lekcja 14
Temat: Czy już umiem – ułamki zwykłe
Cel: sprawdzę swoje umiejętności związane z ułamkami zwykłymi.
Przyszedł czas na sprawdzenie, czego nauczyliście się o ułamkach zwykłych.
Przygotujcie kartkę w kratkę.
Na górze kartki napiszcie: imię i nazwisko, klasa, poniżej Kartkówka – ułamki zwykłe
Przeczytajcie uważnie polecenia i napiszcie rozwiązania poniższych zadań.
Po rozwiązaniu i sprawdzeniu swoich rozwiązań, kartkę włóżcie do przygotowanej specjalnie w tym celu teczki, koszulki, koperty lub w inne miejsce, gdzie będziecie gromadzić swoje prace.
Zdjęcie lub skan pracy prześlijcie swojej nauczycielce do sprawdzenia. Na odesłanie pracy macie 2 dni robocze od dnia, w którym przewidziana jest kartkówka, czyli do wtorku, godz.20:00
Jeśli nie możecie odesłać pracy w tym terminie, to koniecznie skontaktujcie się ze swoją nauczycielką matematyki.

*Wersja do wydruku Lekcja 14 -Czy już umiem – Ułamki zwykłe
Tydzień obowiązywania: 15 – 17 kwietnia 2020 r.
Lekcja 9
Temat: Porównywanie niektórych ułamków
Cel: umiem porównywać ułamki o takich samych mianownikach i ułamki o takich samych licznikach.
Umiesz już porównywać liczby naturalne, a na tej lekcji nauczysz się jak porównywać niektóre ułamki zwykłe.
Przyjrzyj się dokładnie ilustracji z czekoladą na str. 74 podręcznika i trzem ilustracjom poniżej.
Aby jeszcze lepiej zrozumieć porównywanie ułamków o takich samych mianownikach obejrzyj filmik:
https://www.youtube.com/watch?v=xGhhTqX7COE
Przepisz do zeszytu zdanie z niebieskiej ramki na stronie 74 i wykonaj ilustrujący je rysunek – może być ten z kołami lub kwadratami, możesz też wykonać inny rysunek, według własnego pomysłu.
Wykonaj przykłady a, b, c z zad. 1 ze str. 75
Przyjrzyj się rysunkom: w dolnej części str. 74 i na str. 75;
Aby jeszcze lepiej zrozumieć porównywanie ułamków o takich samych licznikach obejrzyj filmik:
https://www.youtube.com/watch?v=cXH77pNdhx4
Przepisz do zeszytu zdanie z niebieskiej ramki na stronie 75 i wykonaj ilustrujący je rysunek – może być ten z kołami lub kwadratami, możesz też wykonać inny rysunek, według własnego pomysłu.
Wykonaj przykłady d, e, f z zad. 1 ze str. 75
Wykonaj zad. 2 ze str.75
*Wersja do wydruku Lekcja 9 – porównywanie niektórych ułamków
Lekcja 10
Temat. Skracanie i rozszerzanie ułamków
Cel: umiem skracać i rozszerzać ułamki zwykłe.
Z umiejętności, którą masz zdobyć na tej lekcji będziesz wielokrotnie korzystać później – ułatwia ona wykonywanie innych obliczeń.
Wykonaj w zeszycie rysunki prostokątów według poleceń w podręczniku w „Na dobry początek” ze str. 77.
Co zauważasz?
Przeanalizuj rysunek i opis w dolnej części str. 77 i górnej części str. 78.
Omówione tu czynności to rozszerzanie ułamków
W utrwaleniu tej umiejętności może pomóc Ci filmik:
https://www.youtube.com/watch?v=RvGnir0s1c4
Przepisz do zeszytu pierwszy z tekstów na niebieskim tle na str. 78
Wykonaj cztery dowolnie wybrane przykłady z poziomu A zad. 1 ze str. 80
Przeanalizuj tekst zapisany poniżej przepisanego przez Ciebie. Dotyczy on skracania ułamków.
Warto obejrzeć obrazujący tę czynność filmik:
https://www.youtube.com/watch?v=8ZkXz0Rw7jI
Przepisz do zeszytu drugi z tekstów na niebieskim tle (str. 78)
Wykonaj cztery dowolnie wybrane przykłady z poziomu B zad. 1 ze str. 80
*Wersja do wydruku Lekcja 10 – skracanie i rozszeranie ułamków
Tydzień obowiązywania: 06 – 08 kwietnia 2020 r.
Lekcja 7
Temat: Ułamek jako część całości
Cel: – umiem opisywać część danej całości za pomocą ułamka
Na dzisiejszej lekcji zapoznasz się z pojęciem ułamka zwykłego.
Będziesz spotykać się z nim bardzo często – przez wszystkie lata nauki matematyki
i w sytuacjach praktycznych, dlatego bardzo ważne jest dobre zrozumienie jego sensu.
Zadania do wykonania:
Zapoznaj się dokładnie z ilustracją na str. 66 podręcznika, wykonaj polecenia.
Przeczytaj bardzo uważnie wyjaśnienia na str. 67
Zapisz w zeszycie:
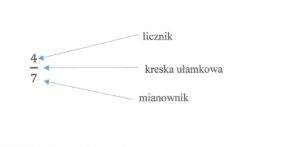
mianownik – informuje na ile równych części podzielono całość
licznik – informuje ile części wybieramy
Dla lepszego zrozumienia przeanalizuj przykłady przedstawione na str. 68
Wykonaj zadania 1 i 2 ze str. 69, 5 i 8 ze str. 70 (w zad. 5 d, e, f podziel sobie najpierw figury na równe części) .
* Wersja do wydruku Lekcja 7 -Ułamek jako część całości
Lekcja 8
Temat: Ułamek na osi liczbowej
Cel: – umiem odczytywać ułamki zaznaczone na osi liczbowej
– umiem zaznaczać ułamki na osi liczbowej
Umiesz już zaznaczać liczby naturalne na osi liczbowej dobierając odpowiednią jednostkę
i odczytywać zaznaczone.
Jeśli chcesz możesz sobie to przypomnieć oglądając filmik https://www.youtube.com/watch?v=pBcHzlcv1Ag
W przypadku ułamków bardzo istotne jest dobranie właściwej jednostki – tak aby odcinek pomiędzy 0 a 1 był podzielony na tyle równych części, ile wynosi mianownik ułamka.
Zadania do wykonania:
Zapoznaj się uważnie z przykładem drugim na str. 69.
Wykonaj zadania 11 i 12 ze str. 71
*Wersja do wydruku Lekcja 8 – Ułamek na osi liczbowej
Tydzień obowiązywania: 30 marca – 03 kwietnia 2020 r.
Lekcja 3.
Temat: Obliczenia związane ze skalą
Cel: – utrwalam pojęcie skali,
– umiem zastosować zdobytą wiedzę i umiejętności do obliczeń praktycznych.
Znasz już pojęcie skali i umiesz wykonywać proste obliczenia z nią związane, np.:
Jeśli odcinek rzeczywisty ma długość 15 cm, to:
– w skali 1:5 będzie miał długość 15cm : 5 = 3cm,
– w skali 2:1 będzie miał długość 15cm x 2 = 30cm
Zadania do wykonania:
Wykorzystaj te umiejętności do wykonania zadań z podręcznika:
· Zadanie 6 ze str. 51 – wskazówka: zmierz średnice wszystkich monet i sprawdź wykonując odpowiednie dzielenia ile razy dana moneta ma średnicę mniejszą lub większą od średnicy tej, którą wybrałaś/eś jako przedstawioną w rzeczywistej wielkości.
· Zadanie 8 ze str. 51 – wystarczy, że wykonasz dwa rysunki: na jednym przedstawisz wybraną figurę w skali 2:1, a na drugim inną figurę w skali 3:1.
· Zadanie 4 ze str. 58 – wskazówka: na mapie zmierz linijką odległości między wskazanymi miastami, a następnie pomnóż je przez odpowiednią liczbę (najłatwiej będzie Ci obliczyć, jeśli wykorzystasz skalę mianowaną podaną na mapie).
*Wersja do wydruku Lekcja 3 – Obliczenia związane ze skalą
Lekcja 4 i 5
Temat. Powtórzenie – figury geometryczne
Cel: – utrwalam wiadomości o poznanych figurach geometrycznych
Te dwie lekcje wykorzystaj do przypomnienia i utrwalenia tego, czego nauczyłaś/eś się o figurach geometrycznych i uzupełnienia ewentualnych braków.
Zadania do wykonania:
Wykonaj zadania z podręcznika: zad. 1-8 ze str.60
Jeśli dobrze poradziłaś/eś sobie z tymi zadaniami możesz spróbować jeszcze rozwiązać zad. 17 i 18 ze str. 61
Sprawdzaj swoje rozwiązania korzystając z ostatnich stron podręcznika.
W razie problemów pamiętaj, że zawsze możesz skorzystać z wyjaśnień umieszczonych w podręczniku; zwróć uwagę zwłaszcza na zamieszczone tam przykłady; możesz też poprosić o wskazówki nauczycielkę, kontaktując się z nią przez e-mail na Dziennik lub adres podany na tej stronie.
*Wersja do wydruku Lekcja 4 i 5 – powtórzenie, figury geometryczne
Lekcja 6
Temat: Zadania sprawdzające -figury geometryczne
Cel: sprawdzenie wiedzy i umiejętności związanych z figurami geometrycznymi
Rozwiąż poniższe zadania (pamiętaj o dokładnym przeczytaniu treści); nie przepisuj ich treści, ale wyraźnie zaznaczaj numer rozwiązywanego zadania i zapisuj odpowiedzi.
Rozwiązania możesz przesłać do nauczycielki na e-maila, lub skorzystać z aplikacji Teams; możesz też podpisać kartki z rozwiązaniami i zachować je do przekazania po powrocie do szkoły.
Zadanie 1
- Narysuj okrąg o środku w punkcie D i promieniu 3,5 cm.
Uzupełnij zdanie: Średnica tego okręgu ma długość ………………
2. Średnica okręgu o środku w punkcie G wynosi 16 cm.
Uzupełnij zdanie: Promień tego okręgu jest równy ……………
Zadanie 2 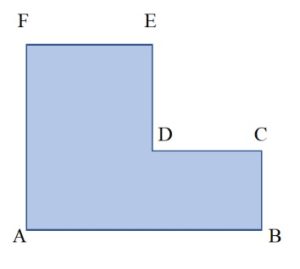
- Nazwij narysowaną figurę.
- Podaj parę boków równoległych.
- Podaj parę boków prostopadłych
Zadanie 3
Długości boków prostokąta wynoszą 11 cm i 7 cm.
- Oblicz obwód tego prostokąta.
- Oblicz długość boku kwadratu, który ma taki sam obwód jak ten prostokąt.
Zadanie 4
Narysuj odcinek AB o długości 6cm oraz odcinek CD dłuższy o 4 cm od odcinka AB oraz odcinek EF dwa razy krótszy od odcinka CD. Zapisz ich długości.
Zadanie 5
Uzupełnij.
a) ……… m ……… cm = 574 cm b) ……… cm …… mm = 76 mm
c) 148 km = ……………… m d) ……… km ………… m = 2781 m
e) 7 km 48 m = ……………m
Zadanie 6
Obwód prostokąta wynosi 42 cm, a jeden z boków ma 6 cm. Oblicz długość drugiego boku prostokąta.
Zadanie 7
- Bok kwadratu narysowanego w skali 3 : 1 ma długość 24 cm. Oblicz rzeczywistą
długość boku tego - Mapa jest sporządzona w skali 1 : 1000. Oblicz rzeczywistą odległość między
kościołem a sklepem, jeżeli na mapie odległość ta wynosi 13 cm i 4 mm.
Zadanie 8
Mama obszyła prostokątną serwetkę i zużyła 2 m 70 cm tasiemki. Kasia narysowała
tę serwetkę w pewnej skali. Jaka jest skala narysowanej serwetki, jeśli rysunek przedstawia prostokąt o wymiarach 4 cm i 5 cm?
*Wersja do wydruku Lekcja 6 – zadania sprawdzające.
Tydzień obowiązywania: 25 – 27 marca 2020 r.
Lekcja 1.
Temat: Skala
Cel:
– rozumiem pojęcie skali;
– wiem, co oznaczają zapisy typu: 1:3, 5: 1, 1:1;
– umiem obliczyć rzeczywistą długość odcinka przedstawionego w podanej skali;
– umiem obliczyć jaką długość w podanej skali będzie miał odcinek o znanej długości.
Zadania do wykonania:
Aby zapoznać się z pojęciem skali przeczytaj uważnie informacje zamieszczone w podręczniku na str. 48 i przyjrzyj się przykładom ze str. 49 i 50
Jeśli nie masz podręcznika w domu, to możesz skorzystać z dostępnego na stronie: ebooki.nowaera.pl/
Możesz też skorzystać z filmików, które znajdziesz pod adresami:
https://pistacja.tv/film/mat00145-skala-wprowadzenie
Zrób notatkę w zeszycie przepisując poniższe zdania uzupełniając wykropkowane miejsca:
- Jeśli jakaś figura została przedstawiona w skali oznacza to, że jej wymiary na rysunku zostały pomniejszone lub ………………………………… w stosunku do rzeczywistych.
- Skala 1: 5 oznacza, że wymiary na rysunku są … razy mniejsze niż w rzeczywistości.
- Skala 4 : 1 oznacza, że wymiary na rysunku są ……razy………………………niż w …………………………
- Skala 1:1 oznacza że wymiary na rysunku są …………………. jak w rzeczywistości.
Dla chętnych:
Jeśli chcesz poćwiczyć możesz skorzystaj z linku:
https://epodreczniki.pl/a/co-to-jest-skala-obliczanie-dlugosci-odcinkow-w-skali/D17oK7GIl
Lekcja 2.
Temat: Mapa i plan
Cel:
– umiem zastosować zdobyte na poprzedniej lekcji umiejętności (pojęcie skali i obliczenia związane ze skalą) do rozwiązywania zadań praktycznych.
– znam różne sposoby zapisu skali (liczbowa, liniowa, mianowana).
Zadania do wykonania:
Zapoznaj się z informacjami przedstawionymi na str. 56 podręcznika.
Jeśli nie masz podręcznika w domu, to możesz skorzystać z dostępnego na stronie: https://ebooki.nowaera.pl/
Przeanalizuj przykłady znajdujące się na str. 57
Pomocny w utrwaleniu wiadomości może być filmik:
https://pistacja.tv/film/mat00148-skala-na-planach-i-mapach
Zrób notatkę w zeszycie przepisując (i przerysowując) ze str. 56 podręcznika przykłady różnego zapisu skali.
Dla chętnych:
Jeśli masz ochotę poćwiczyć, możesz wrócić do strony:
https://epodreczniki.pl/a/co-to-jest-skala-obliczanie-dlugosci-odcinkow-w-skali/D17oK7GIl
*Wersja do wydruku – Lekcja 1 i 2
Sprawdź, czy umiesz!
Zachęcamy do wykonania zadań. Rozwiązania zapisujcie na kartkach. Możecie przesyłać rozwiązane zadania (zeskanowane lub zrobione zdjęcie) jako załączniki na adres swoich nauczycielek:
Mirosława Modzelewska miroslawa_mm@op.pl
Anna Nowak anna.nowak04@gmail.com
Sprawdzimy Wasze prace i wstawimy oceny. Tą drogą możecie też zadawać nam pytania.
Prosimy, pamiętajcie o podpisaniu się na kartce 🙂
Jeśli czegoś zapomnieliście, to kontaktujcie z nami przez dziennik elektroniczny lub mailowo.
23 marca 2020 r.
Temat: Obwód wielokąta.
Zadania do rozwiązania:
19 marca 2020 r.
Temat: Liczby naturalne – rozwiązywanie zadań tekstowych.
Zadania do rozwiązania:
Materiały pomocnicze:
Rozwiązywanie zadań tekstowych
16 marca 2020 r.
Temat: Kolejność wykonywania działań.
Zadania do rozwiązania:
Materiały pomocnicze:
Zaglądajcie też na strony:
Khan Academy – platforma edukacyjna
Matzoo – Matematyczne Zoo – zadania i testy
Pi-stacja – Darmowe wideolekcje z matematyki